1
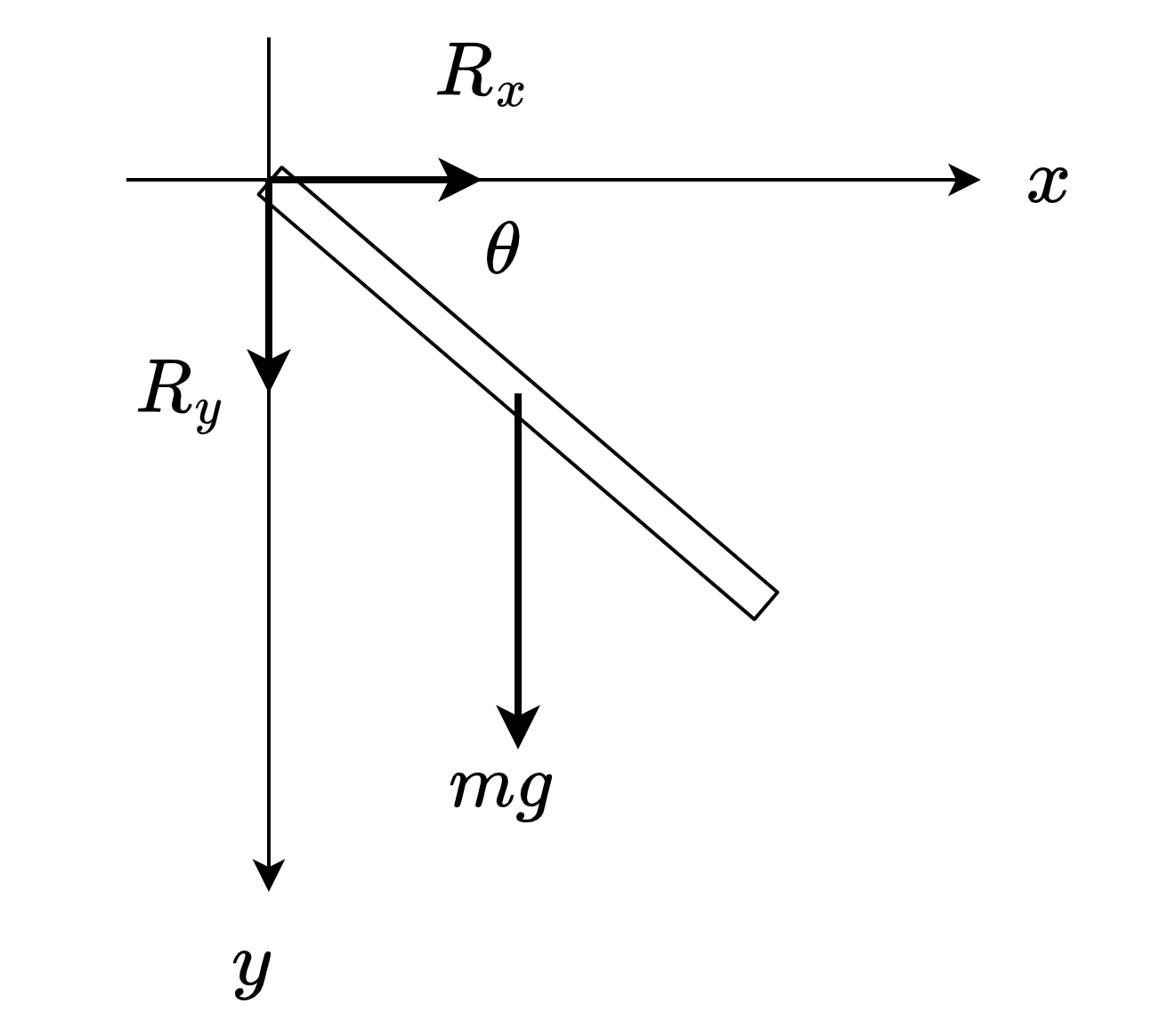
回転運動方程式は
\[ \frac{1}{3}ml^2\ddot{\theta} = -mg\frac{l}{2}\cos \theta \]
となり、重心運動方程式は
\[\begin{align*} m\ddot{x} &= R_x \\ m\ddot{y} &= mg + R_y \end{align*}\]
ここで、\(x,y\) については、
\[\begin{align*} x &= \frac{l}{2} \cos \theta \\ y &= \frac{l}{2} \sin \theta \\ \dot{x} &= -\frac{l}{2} \sin \theta \dot{\theta} \\ \dot{y} &= \frac{l}{2} \cos \theta \dot{\theta} \\ \ddot{x} &= -\frac{l}{2} \cos \theta \dot{\theta}^2 - \frac{l}{2} \sin \theta \ddot{\theta} \\ \ddot{y} &= -\frac{l}{2} \sin \theta \dot{\theta}^2 + \frac{l}{2} \cos \theta \ddot{\theta} \end{align*}\]
以上のことより、重心運動方程式は次のようになる
\[ -m\frac{l}{2} \begin{pmatrix} \cos \theta & \sin \theta \\ -\sin \theta & \cos \theta \end{pmatrix} \begin{pmatrix} \dot{\theta}^2 \\ \ddot{\theta} \end{pmatrix} = \begin{pmatrix} R_x \\ mg + R_y \end{pmatrix} \]
\[ -m\frac{l}{2} \begin{pmatrix} \dot{\theta}^2 \\ \ddot{\theta} \end{pmatrix} = \begin{pmatrix} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{pmatrix} \begin{pmatrix} R_x \\ mg + R_y \end{pmatrix} \]
これが要するに角加速度の導出だったわけだ。 \(\ddot{\theta}\) について無視したら次元の数が足りないとなるだろう?
で、軸に働く力を求めるとなると、上の方程式を解けばいいわけだ。
エネルギー積分によって、
\[ \frac{1}{3}ml^2\ddot{\theta} = -mg\frac{l}{2}\cos \theta \]
を \(0 \to \pi /2\) で積分して、いろいろと式を変形すると、求められていくわけだ。
問題
真空中に,中空で断面積 \(S\)〔\(\text{m}^2\)〕のソレノイドがある。このソレノイドの単位長さあたりの導線の巻数は n〔\(1/\text{m}\)〕であり,導線には電流 \(I\)〔\(\text{A}\)〕の定常電流が流れている。このとき以下の問いに答えよ。ただし真空の透磁率を \(\mu_0\)〔\(\text{N}/\text{A}^2\)〕,円周率を \(\pi\) とし,ソレノイドの長さは十分に長いものとする。
(問 1) ソレノイド内部の磁場(磁界)の強さを求めよ。
このソレノイドの内部全体に,比透磁率 \(\mu_r\) ( \(\gg 1\) )の鉄(鉄芯)を入れた。このとき,次の問いに答えよ。
(問 2) ソレノイド内部の磁場の強さ \(H\)〔\(\text{A}/\text{m}\)〕と磁束密度を求めよ。
(問 2)と同じ鉄芯が入った同じソレノイドを,図 1 のように,その中心が半径 \(R\)〔\(\text{m}\)〕の円環を描くように均一に曲げて鉄芯の端を接続した。ソレノイドには電流 \(I\)〔\(\text{A}\)〕が流れているとして,以下の問いに答えよ。
(問 3) ソレノイド全体の巻数 \(N\) と \(H,R,I\) の間に成り立つ関係式を,これらを用いて表せ。