化学反応速度論
化学反応速度
化学反応速度とは、単位時間あたりに反応物質が反応する速さのことを指す。これは反応物質の濃度に依存するため、一般的には濃度の関数として表される。
\[
-r_A = - \dv{C_A}{t} = f(C_A, C_B, \cdots)
\]
ここで考える反応装置とは回分反応器(バッチ式)で、これの特徴は、閉じた系であること、反応物質の濃度が空間的に均一であること、反応物質の濃度が時間的に変化することである。
他にも、槽型反応器CSTR、管型流通式反応機などがある。CSTRは特に大量生産に向いているので、工業的によく使われる。
ある均一反応を考えると、その反応速度は以下のように表される。
\[
\ce{aA + bB -> cC + dD}
\]
Aの消失速度は
\[
-r_A = \frac{1}{V} \dv{N_A}{t} \; \left[\frac{\text{mol}}{\text{m}^3 \cdot \text{s}}\right]
\]
また、次のような等式も当然成り立つ。
\[
\frac{r_A}{a}= \frac{r_B}{b} = \frac{r_C}{c} = \frac{r_D}{d}
\]
反応の種類
\[
\ce{A -> B}
\]
\[
\ce{A + B -> C + D}
\]
\[
\ce{A -> B -> C}
\]
\[
\ce{A -> C}
\]
\[
\ce{A -> D}
\]
\[
\ce{A + B -> C}
\]
分解できる最小単位を素反応と呼ぶ。
\[
\ce{H2 + Br2 -> 2HBr}
\]
\[
r_{\ce{HBr}} = \frac{k_1[\ce{H2}][\ce{Br2}]^{\frac{1}{2}}}{k_2 + \frac{[\ce{HBr}]}{[\ce{Br2}]}}
\]
反応速度式
\[
-r_A=kC_A^aC_B^b \cdots
\]
ここで、\(k\) は反応速度定数である。また、\(a,b,\cdots\) は反応次数である。全体の反応次数は \(a+b+\cdots\) である。また、反応次数は整数とは限らなし、 \(0\) であることもある。
例として幾つかあげる。
- \[
\ce{H2+I2 -> 2HI}
\]
\[
r = k[\ce{H2}][\ce{I2}]
\]
- \[
\ce{CH3CHO -> CH4 + CO}
\]
\[
r = k[\ce{CH3CHO}]^{3/2}
\]
- \[
\ce{H2 + Br2 -> 2HBr}
\]
\[
r_{\ce{HBr}} = \frac{k_1[\ce{H2}][\ce{Br2}]^{\frac{1}{2}}}{k_2 + \frac{[\ce{HBr}]}{[\ce{Br2}]}}
\]
以上のように、実験的に決定することとなる。
このような手順を繰り返してある一定の反応速度式を求めては繰り返す作業で、反応機構を求めることを反応機構解析と呼ぶ。
定常状態近似
- 正味の変化速度は各々の素反応での反応速度の総和で表される。
- 反応中間体の変化量は \(0\) である。
このような近似を定常状態近似と呼ぶ。このような近似を用いて解析した結果を一つ例として出すと、
\[
\ce{H2 + Br2 -> 2HBr}
\]
この反応の速度式は実験的に次のようになっている。
\[
r_{\ce{HBr}} = \frac{k_1[\ce{H2}][\ce{Br2}]^{\frac{1}{2}}}{k_2 + \frac{[\ce{HBr}]}{[\ce{Br2}]}}
\]
この反応の素反応は次のようになっている。
- \(\ce{Br2 -> 2Br^{\ast}}\)
- \(\ce{H2 + Br^{\ast} -> HBr + H^{\ast}}\)
- \(\ce{H^{\ast} + Br2 -> HBr + Br^{\ast}}\)
- \(\ce{H^{\ast} + HBr -> H2 + Br^{\ast}}\)
- \(\ce{Br^{\ast} + Br^{\ast} -> Br2}\)
なので、
\[
\dv{[\ce{HBr}]}{t} = k_2[\ce{Br^{\ast}}][\ce{H2}] + k_3[\ce{H^{\ast}}][\ce{Br2}] - k_4[\ce{H^{\ast}}][\ce{HBr}]
\]
\[
\dv{[\ce{Br^{\ast}}]}{t} = k_1[\ce{Br2}] - k_2[\ce{Br^{\ast}}][\ce{H2}] + k_3[\ce{H^{\ast}}][\ce{Br2}] + k_4[\ce{H^{\ast}}][\ce{HBr}] - k_5[\ce{Br^{\ast}}]^2 =0
\]
\[
\dv{[\ce{H^{\ast}}]}{t} = k_2[\ce{Br^{\ast}}][\ce{H2}] - k_3[\ce{H^{\ast}}][\ce{Br2}] - k_4[\ce{H^{\ast}}][\ce{HBr}] = 0
\]
この式をこねくり回すことによって、反応速度式を求めることができる。その内容は下二つの式の中間体濃度を消去することで求めることができる。
次に反応機構の推察をしてみる。これは試験で出すらしい。
\[
\ce{2A + B -> A2B}
\]
これの反応速度式が
\[
r = \frac{0.72[\ce{A}]^2[\ce{B}]}{1+2[\ce{A}]}
\]
とする。
この反応の素反応を、
\[
\ce{A + A + B <=> A2^{\ast} + B <=> A2B}
\]
と考えて、反応速度式を求めると、おかしくなる。どうおかしくなるかは面倒なので具体的には書かない。めんどくさい
\[
\ce{A + A + B <=> AB + A <=>A2B}
\]
にするとうまいこといく。
Linndemann-Hinshelwood機構
気相中での化学分解や異性化反応をモデル化で使われる。
\[\ce{A -> P}\]
この一見一時反応見えるものが実は中間体の存在する反応だという反応機構だ。
\[\ce{A + M <=> A^{*} + M}\]
\[\ce{A^{*} -> P}\]
ここで、 \(\ce{M}\) は触媒や溶媒のことを指す。 \(\ce{A^{*}}\) は中間体である。
この反応の速度式は次のように表される。
\[ k_1[\ce{A}][\ce{M}] = k_{-1}[\ce{A^*}][\ce{M}] + k_2[\ce{A^*}] \]
\[ \Rightarrow \quad [\ce{A^*}] = \dfrac{k_1[\ce{A}][\ce{M}]}{k_{-1}[\ce{M}] + k_2} \]
で、全体の反応速度は \(k_2 [\ce{A^*}]\) で表されるので、
\[
\dv{[\ce{P}]}{t} = k_2 [\ce{A^*}] = \frac{k_1k_2[\ce{A}][\ce{M}]}{k_{-1}[\ce{M}] + k_2}
\]
この式で、\(k_{-1}[\ce{M}] \gtreqless k_2\) によって一次反応なのか二次反応なのかが決まる。
また、見なしの反応速度定数を \(k\) とかにしたら、
\[
\begin{aligned}
k[\ce{A}] &= \frac{k_1k_2[\ce{A}][\ce{M}]}{k_{-1}[\ce{M}] + k_2} \\
\dfrac{1}{k} &= \dfrac{k_{-1}}{k_1k_2} + \dfrac{1}{k_2[\ce{M}]}
\end{aligned}
\]
ここで、
\[
\begin{aligned}
p&=\dfrac{n}{V}RT=[\ce{M}]RT \\
\dfrac{1}{[\ce{M}]} &\propto \dfrac{1}{p}
\end{aligned}
\]
ということから考えれば、
\[
\dfrac{1}{k} \propto \dfrac{1}{p}
\]
このように、反応速度定数は圧力に依存することがわかる。
酵素反応
酵素で反応が活性化される反応物を基質と呼ぶ。
\[
\ce{S ->[\symup{enzyme}] P}
\]
反応速度は酵素濃度に比例し、また、基質濃度が高い時は、反応速度は基質濃度によらず一定である。
反応速度式は次のような素反応で考えられるする。
\[
\ce{E + S <=>[k_1][k_2] ES ->[k_3] E + P}
\]
$ $ は酵素基質複合体と呼ばれる。
\[
\begin{aligned}
\dv{[\ce{ES}]}{t} &= k_1[\ce{E}][\ce{S}] - k_2[\ce{ES}] - k_3[\ce{ES}] = 0\\
\ce{E_0} &= [\ce{E}] + [\ce{ES}] \\
\end{aligned}
\]
ここで、 $ $ を求めれば、酵素が優れているかどうかがわかる。ただし、 \(\ce{E}\) は邪魔なので消してやると、
\[
[\ce{ES}] = \frac{[\ce{E_0}][\ce{S}]}{\frac{k_2+k_3}{k_1} + [\ce{S}]} = \frac{[\ce{E_0}][\ce{S}]}{k_m + [\ce{S}]}
\]
となる。ここで、 \(k_m = \frac{k_2+k_3}{k_1}\) とする。この式はミカエリス・メンテンの式と呼ばれ、 \(k_m\) はミカエリス定数と呼ばれる。優れている酵素ほど \(k_m\) が小さい。
次に最大反応速度は
\[
V_{\max} = k_3[\ce{E_0}]
\]
なのは明らかである。そのように置いておくと、
\[
\dv{[\ce{P}]}{t} = k_3[\ce{ES}] = \frac{V_{\max}[\ce{S}]}{k_m + [\ce{S}] }
\]
この時、 \(k_m\) は反応速度の最大値の半分となる \([\ce{S}]\) の値と同じなのは \(k_m = [\ce{S}]\) 代入したらすぐわかる。なのでそこを基準点として考えて、
- \([\ce{S}] \ll k_m\) の時、 \(\dv{[\ce{P}]}{t} = \frac{V_{\max}}{k_m}[\ce{S}]\) となる。
- \([\ce{S}] \gg k_m\) の時、 \(\dv{[\ce{P}]}{t} = V_{\max}\) となる。
また、 \(V_{\max}\) の中身を考えれば、 \(\dv{[\ce{P}]}{t}\) は常に \([\ce{E_0}]\) に比例することがわかる。
次に、 \(k_m\) の実験的な求め方だが、式を分母分子逆転させて考える。それで直線プロットする。
重合反応
\[
\begin {aligned}
\ce{I &->[k_d] 2R^{.}}\\
\ce{R^{.} + M &->[k_i] M^{.}}\\
\ce{M^{.} + M &->[k_p] M^{.}}\\
\ce{2M^{.} &->[k_t] P}\\
\ce{M^{.} + S &->[k_{tr}] P + S^{.}}
\end{aligned}
\]
重要なのは、 \(\ce{M}\) はモノマーではあるが、2式以降の \(\ce{M^{.}}\) はラジカルで、ただのモノマーじゃない。
ポリマーの生成速度はモノマーの減少速度に等しい。
\[
R_p = \dv{[\ce{P}]}{t} = k_p[\ce{M^{.}}][\ce{M}]
\]
それからラジカルは定常状態にあると仮定するので、
\[
\begin{aligned}
\dv{[\ce{M^{.}}]}{t} &= k_i[\ce{R^{.}}][\ce{M}] - k_t[\ce{M^{.}}]^2 = 0\\
\dv{[\ce{R}]}{t} &= 2fk_d[\ce{I}] - k_i[\ce{R^{.}}][\ce{M}] = 0
\end{aligned}
\]
これを解くと、
\[
R_p = \sqrt{\frac{2fk_d}{k_t}}k_p[\ce{I}]^{1/2}[\ce{M}]
\]
動力学的鎖長は
\[
\nu = \frac{\text{単位時間に消えたモノマー分子}}{\text{単位時間に生成されたポリマー分子}}=\frac{R_p}{R_{tr}+R_t}
\]
これを計算すると、
\[
\begin{aligned}
\frac{1}{\nu} &= \frac{R_t}{R_p} + \frac{R_{tr}}{R_p} \\
&= \frac{k_t[\ce{M^{.}}]}{k_p[\ce{M^{.}}][\ce{M}]} + \frac{k_{tr}[\ce{M^{.}}][\ce{S}]}{k_p[\ce{M^{.}}][\ce{M}]} \\
&= \frac{k_t}{k_p} + \frac{k_{tr}[\ce{S}]}{k_p[\ce{M}]} \\
&= \frac{1}{\nu_0} + C_{tr}\frac{[\ce{S}]}{[\ce{M}]}
\end{aligned}
\]
ここで \(\nu_0\) は溶媒がない時の動力学的鎖長で、 \(C_{tr}\) は \(k_{tr}/k_p\) で連載同定数と呼ばれる。
反応速度と温度
反応速度定数は温度に依存する。これはアレニウスの式で表される。
\[
k = A\exp\left(-\frac{E_a}{RT}\right)
\]
ここで、 \(A\) は頻度因子、 \(E_a\) は活性化エネルギー、 \(R\) は気体定数、 \(T\) は温度である。
この式を対数変換すると、
\[
\ln k = \ln A - \frac{E_a}{RT}
\]
これの直線プロットをアレニウスプロットよ呼ぶ。
積分法
反応速度係数を求める方法の一つに積分法がある。
\[
\begin{aligned}
r= - \dv{C_A}{t} &= kf(C_A) \\
-\dv{C_A}{f(C_A)} &= kdt \\
\int_{C_{A0}}^{C_A} \frac{dC_A}{f(C_A)} &= -kt
\end{aligned}
\]
具体的には、
\[
\begin{aligned}
\int_{C_{A0}}^{C_A} \frac{dC_A}{C_A} &= -kt\\
\ln \frac{C_A}{C_{A0}} &= -kt
\end{aligned}
\]
反応率
\[
X=\frac{C_{A0}-C_A}{C_{A0}}
\]
を使って表すと
\[
\ln(1-X) = kt
\]
となる。ここで半減期がわかったとすると、
\[
k = \frac{\ln 2}{t_{1/2}}
\]
と、反応速度定数がわかる。
同様にして積分すればいい。
\[
\begin{aligned}
\int_{C_{A0}}^{C_A} \frac{dC_A}{C_A^2} &= -kt\\
- \frac{1}{C_A} + \frac{1}{C_{A0}} &= -kt\\
\frac{1}{C_A} &= \frac{1}{C_{A0}} + kt
\end{aligned}
\]
で、半減期は
\[
t_{1/2} = \frac{1}{kC_{A0}}
\]
になって、初期濃度に依存するようになる。
\[
\begin{aligned}
\int_{C_{A0}}^{C_A} \frac{dC_A}{C_A^n} &= -kt\\
\frac{1}{(n-1)C_A^{n-1}} - \frac{1}{(n-1)C_{A0}^{n-1}} &= kt\\
\frac{1}{C_A^{n-1}} &= \frac{1}{C_{A0}^{n-1}} + (n-1)kt
\end{aligned}
\]
\[
\begin{aligned}
\int_{C_{A0}}^{C_A} dC_A &= -kt\\
C_A - C_{A0} &= -kt\\
C_A &= C_{A0} - kt
\end{aligned}
\]
\[
\ce{A + B -> X}
\]
\[
\begin{aligned}
\dv{[\ce{A_0}] - [\ce{X}]}{t} &= -k([\ce{A_0}] - [\ce{X}])([\ce{B_0}] - [\ce{X}]) \\
\dfrac{\dd{} [\ce{X}]}{([\ce{A_0}] - [\ce{X}])([\ce{B_0}] - [\ce{X}])} &= kdt \\
\ln \frac{[\ce{A_0}] - [\ce{X}]}{[\ce{B_0}] - [\ce{X}]} &= kt
\end{aligned}
\]
後半戦 (昔のやつ)
不均一反応
不均一反応の速度表示には次のようなものがある
| \(r_i\) |
\(-\dfrac{1}{V}\dfrac{d}{dt}n_i\) |
\(\mathrm{mol \cdot m^{-3} \cdot s^{-1}}\) |
単位時間あたりの体積反応量 |
| \(r_i'\) |
\(-\dfrac{1}{W}\dfrac{d}{dt}n_i\) |
\(\mathrm{mol \cdot kg^{-1} \cdot s^{-1}}\) |
単位時間あたりの質量反応量 |
| \(r_i''\) |
\(-\dfrac{1}{S}\dfrac{d}{dt}n_i\) |
\(\mathrm{mol \cdot m^{-2} \cdot s^{-1}}\) |
単位時間あたりの表面反応量 |
これらはすべて互換可能である。
\[
r_i = \dfrac{W}{V}r_i' = \dfrac{S}{V}r_i''
\]
ここで、 \(W\) は質量、 \(S\) は表面積、 \(V\) は体積である。
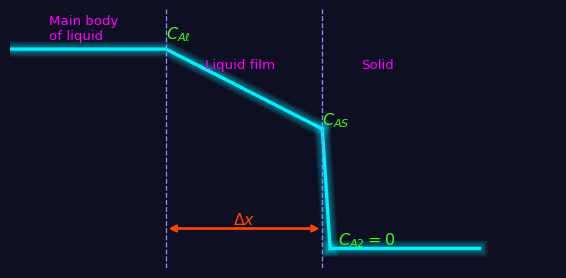
固液界面における反応
Show Code
import matplotlib.pyplot as plt
import numpy as np
# プロファイルのxとy座標を設定
x_vals = [0.0, 0.2, 0.4, 0.41, 0.6]
y_vals = [1.0, 1.0, 0.6, 0.0, 0.0] # Solid内部でC_A2=0
x_vals1 = x_vals[:3]
y_vals1 = y_vals[:3]
x_vals2 = x_vals[2:4]
y_vals2 = y_vals[2:4]
x_vals3 = x_vals[3:]
y_vals3 = y_vals[3:]
# グローエフェクト設定
n_lines = 10
diff_linewidth = 1.05
alpha_value = 0.05
neon_blue = '#00f0ff'
# 図と軸のセットアップ
fig, ax = plt.subplots(figsize=(6, 3))
fig.patch.set_facecolor('#0f0f23') # 背景
ax.set_facecolor('#1a1a2e') # プロットエリア背景
# グロー部分
for n in range(1, n_lines + 1):
lw = 2 + (diff_linewidth * n)
ax.plot(x_vals1, y_vals1, color=neon_blue, linewidth=lw, alpha=alpha_value, zorder=1)
ax.plot(x_vals2, y_vals2, color=neon_blue, linewidth=lw, alpha=alpha_value, zorder=1)
ax.plot(x_vals3, y_vals3, color=neon_blue, linewidth=lw, alpha=alpha_value, zorder=1)
# メイン線
ax.plot(x_vals1, y_vals1, color=neon_blue, linewidth=2.5, zorder=2)
ax.plot(x_vals2, y_vals2, color=neon_blue, linewidth=2.5, zorder=2)
ax.plot(x_vals3, y_vals3, color=neon_blue, linewidth=2.5, zorder=2)
# ラベル類
label_color = '#39ff14'
ax.text(0.2, 1.05, r'$C_{A\ell}$', fontsize=12, color=label_color)
ax.text(0.4, 0.62, r'$C_{AS}$', fontsize=12, color=label_color)
ax.text(0.42, 0.02, r'$C_{A2}=0$', fontsize=12, color=label_color)
ax.text(0.05, 1.05, 'Main body\nof liquid', fontsize=10, color='#ff00ff')
ax.text(0.25, 0.9, 'Liquid film', fontsize=10, color='#ff00ff')
ax.text(0.45, 0.9, 'Solid', fontsize=10, color='#ff00ff')
# Δx の矢印とラベル
ax.annotate('', xy=(0.2, 0.1), xytext=(0.4, 0.1),
arrowprops=dict(arrowstyle='<->', color='#ff4500', linewidth=2))
ax.text(0.3, 0.12, r'$\Delta x$', ha='center', fontsize=12, color='#ff4500')
# 縦線(界面と固体開始点)
ax.axvline(x=0.2, color='#8888ff', linewidth=1, linestyle='--')
ax.axvline(x=0.4, color='#8888ff', linewidth=1, linestyle='--')
# 軸非表示と範囲調整
ax.axis('off')
ax.set_xlim(0, 0.7)
ax.set_ylim(-0.1, 1.2)
plt.tight_layout()
plt.show()
このグラフで考える。縦軸は濃度で、横軸は位置である。
Interfaceの部分では、Fickの法則による拡散が起きている。
\[
r_i = -D\frac{dC}{dx} = -D\frac{C_{AS}-C_{AE}}{\Delta x} = - k_{\text{diff}}(C_{AS}-C_{AE})
\]
次に、固体表面では、化学反応が起きている。定常状態なので、反応速度は等しいから、
\[
r_i = k_{\text{rxn}}C_{AS}
\]
これで、見なしの速度定数 \(k\) が \(r_i = kC_{AE}\) と定義されるので、
\[
\frac{1}{k} = \frac{1}{k_{\text{rxn}}} + \frac{1}{k_{\text{diff}}}
\]
となる。この式ってのは、どちらが律速になるのかというのを判断するのにかなり有効である。
このモデルでは固体内での拡散は考えていない。固体の中での濃度分布というのは、のちに語るThieleモジュールとか、Weisz-Prater基準とか (Section 1.3.9) って話題と関連がある。
触媒反応(Langmuir-Hinshelwood)
触媒(固体)表面上で起こる流体反応には、以下のような一連のステップがあり、最も遅いステップが律速段階(律速ステップ)となる。
- 流体バルク中から固体外表面への移動(バルク拡散)
- 外表面から細孔内表面までの孔内拡散
- 反応物の固体表面への吸着
- 固体表面上での化学反応
- 生成物の表面からの脱着
- 孔内から外表面への拡散(生成物の孔内拡散)
- バルクへの生成物輸送(バルク拡散)
Langmuir-Hinshelwood式は3→5の部分をモデル化している。表面被覆率を \(\theta\) とすると、3の部分からして、
\[
r_{\text{ads}} = k_{\text{ads}}(1-\theta)p
\]
となる。ここで、\(p\) は反応物の圧力である。これに合わせて、5の部分は
\[
r_{\text{des}} = k_{\text{des}}\theta
\]
となる。並行状態なので、
\[
r = r_{\text{ads}} = r_{\text{des}}
\]
となる。これを解くと、
\[
\theta = \frac{k_{\text{ads}}p}{k_{\text{des}} + k_{\text{ads}}p}
\]
となる。ここで吸着平衡定数 \(K_{\text{ads}} = k_{\text{ads}}/k_{\text{des}}\) を用いると、
\[
\theta = \frac{K_{\text{ads}}p}{1 + K_{\text{ads}}p}
\]
となる。以下にグラフ化するが、\(p\) の代わりに濃度も同じことができる。
Show Code
import plotly.graph_objects as go
import numpy as np
# 濃度範囲
C = np.linspace(0, 10, 200)
K_values = [0.5, 1.0, 2.0]
colors = ['orange', 'tomato', 'crimson']
# Langmuir吸着等温線(θ)
fig_theta = go.Figure()
for K, color in zip(K_values, colors):
theta = (K * C) / (1 + K * C)
fig_theta.add_trace(go.Scatter(x=C, y=theta, mode='lines',
name=f'K = {K}', line=dict(color=color)))
fig_theta.update_layout(title='Langmuir吸着等温線(被覆率 θ)',
xaxis_title='濃度 C',
yaxis_title='被覆率 θ',
template='plotly_dark')
fig_theta.show()
飽和吸着量を \(q_m\) とすると、
\[
\theta = \frac{q}{q_m}
\]
となる。これを代入すると、
\[
\begin{aligned}
q &= \frac{K_{\text{ads}}p}{1 + K_{\text{ads}}p}q_m \\
\frac{1}{q} &= \frac{1}{q_m} + \frac{1}{K_{\text{ads}}q_m} \frac{1}{p}
\end{aligned}
\]
となる。これをLangmuirプロットと呼ばれる。
解離吸着の場合のLangmuir-Hinshelwood式
解離吸着の場合のLangmuir-Hinshelwood式は、次のように導出される。
\[
r_{\text{ads}} = k_{\text{ads}}(1-\theta)^2p
\]
となる。空いてる穴が二つ必要だから、2乗されている。ここで、\(p\) は反応物の圧力である。これに合わせて、5の部分は
\[
r_{\text{des}} = k_{\text{des}}\theta^2
\]
となる。これも同様に、塞がっている穴二つ必要だから、2乗されている。並行状態なので、
\[
r = r_{\text{ads}} = r_{\text{des}}
\]
となる。これを解くと、
\[
\theta = \frac{\sqrt{k_{\text{ads}}p}}{\sqrt{k_{\text{des}}} + \sqrt{k_{\text{ads}}p}} = \frac{\sqrt{{Kp}}}{\sqrt{Kp} + 1}
\]
となる。
\[
\begin{aligned}
K &= \frac{k_{\text{ads}}}{k_{\text{des}}} \\
&= \frac{\theta^2}{(1-\theta)^2p}
\end{aligned}
\]
っていうのが導出の仕方だけど、質量作用の法則を考えれば、
\[
K = \frac{[\ce{AS}]^2}{[\ce{A2}][\ce{S}]^2}
\]
となる。ここで、 \([\ce{AS}]\) は \(\theta\) に比例して、 \([\ce{S}]\) は \(1-\theta\) に比例する。だから、
\[
K = \frac{\theta^2}{(1-\theta)^2p}
\]
となるという導き方が簡単だ。……導出過程で色々スキップはしてしまってるので解答では使わないように。
2分子吸着の場合のLangmuir-Hinshelwood式
\[
\begin{aligned}
r_{\rm ads,A} &= k_{\rm ads,A}\,(1 - \theta_A - \theta_B)\,p_A,\\
r_{\rm des,A} &= k_{\rm des,A}\,\theta_A,\\
r_{\rm ads,B} &= k_{\rm ads,B}\,(1 - \theta_A - \theta_B)\,p_B,\\
r_{\rm des,B} &= k_{\rm des,B}\,\theta_B.
\end{aligned}
\]
となる。定常状態なので、
\[
\begin{aligned}
r_{\rm ads,A} &= r_{\rm des,A} \\
r_{\rm ads,B} &= r_{\rm des,B}
\end{aligned}
\]
となる。これを解くと、
\[
\begin{aligned}
\theta_A &= \frac{K_A\,p_A}{\,1 + K_A\,p_A + K_B\,p_B\,} \\
\theta_B &= \frac{K_B\,p_B}{\,1 + K_A\,p_A + K_B\,p_B\,}
\end{aligned}
\]
となる。
これについても、質量作用の法則で
\[
K = \frac{[\ce{AS}]}{[\ce{A}][\ce{S}]}
\]
となる。ここで、 \([\ce{AS}]\) は \(\theta_A\) に比例して、 \([\ce{A}]\) と \([\ce{S}]\) は \(1-\theta_A-\theta_B\) に比例する。だから、
\[
K_A = \frac{\theta_A}{(1-\theta_A-\theta_B)p_A}
\]
とできるが……。まあ、式の確認に使おう。
吸着エンタルピー
\[
K = \frac{\theta}{(1 - \theta)p}
\]
となる。ここで、対数をとって、
\[
\ln K = \ln \theta - \ln (1 - \theta) - \ln p
\]
となる。これを \(\theta\) 固定すると、
\[
\pdv{\ln K}{T} + \pdv{\ln p}{T} = 0
\]
となる。ここで \[
K = \exp \qty(\frac{-\Delta G}{RT}) = \exp \qty(-\frac{\Delta H_{\text{ads}}-T\Delta S_{\text{ads}}}{RT})
\]
を代入すると、
\[
\begin{aligned}
\ln K &= -\frac{\Delta H_{\text{ads}}}{RT} + \frac{\Delta S_{\text{ads}}}{R} \\
\pdv{\ln K}{T} &= \frac{\Delta H_{\text{ads}}}{RT^2} \\
\pdv{\ln p}{T} &= -\frac{\Delta H_{\text{ads}}}{RT^2} \\
\pdv{\ln p}{(1/T)} &= \frac{\Delta H_{\text{ads}}}{R}
\end{aligned}
\]
となる。これによって、ある温度において被覆率が一定になるような圧力を実験的に求め、プロットすることによって、吸着エンタルピーを求めることができる。
Wigner-Polanyiの関係式
ここでは表面からの 脱離 について考えている。あと、講義資料と違って、1molあたりのエネルギーで考えているので、 \(k_B\) ではなく、\(R\) を使っている。
とりあえず式としての形は
\[
\begin{aligned}
r_{\text{des}} &= - \dv{\theta}{t} = k \theta^n \\
&= \nu_n \theta^n \exp \qty(-\frac{E_n}{RT})
\end{aligned}
\]
となる。ここで、\(k\) は速度定数で、\(n\) は反応次数で、\(\nu_n\) は頻度因子である。
これの導出については、とりあえず質量作用の法則に従った形だということは覚えておけばいいのだが、 \(\nu_n\) などについての詳しいことは、TSTなどの話に任せた方が良さそう。はっきり言って、講義内の資料で理解するのは不可能と思われる。
TPDデータ
TPDは、Temperature Programmed Desorptionの略で、温度を変化させることによって、吸着している分子が脱離する過程を観察する手法である。
ここでは、TPDデータによるRedhead法について話す。
温度を一定速度 \(\beta=dT/dt\) で上げるとき、
\[
T(t) = T_0 + \beta\,t
\quad\Longrightarrow\quad
\frac{d\theta}{dt}
= \beta\,\frac{d\theta}{dT}
\]
脱離速度 \(r_{\rm des}(T)\) が最大をとる温度 \(T_{\rm max}\) は
\[
\frac{d}{dT}\bigl[r_{\rm des}(T)\bigr]_{T=T_{\rm max}} = 0
\]
でもとまる。
$$
\[\begin{aligned}
-\beta \dv{\theta}{T} &= \nu \theta \exp\!\Bigl(-\frac{E_{\rm des}}{R\,T}\Bigr) \\
\dv{r_{\rm des}}{T} &= \dv{}{T} \dv{\theta}{t} = \dv{}{T} \beta \dv{\theta}{T} = \beta \dv[2]{\theta}{T} \\
\beta \dv[2]{\theta}{T} &= -\nu \dv{\theta}{T} \exp\!\Bigl(-\frac{E_{\rm des}}{R\,T}\Bigr) - \nu \theta \exp\!\Bigl(-\frac{E_{\rm des}}{R\,T}\Bigr) \frac{E_{\rm des}}{R\,T^2} = 0 \\
0 &= \dv{\theta}{T} + \frac{E_{\rm des}}{R\,T^2}\theta \\
&=-\frac{\nu}{\beta} \theta \exp\!\Bigl(-\frac{E_{\rm des}}{R\,T}\Bigr) + \frac{E_{\rm des}}{R\,T^2}\theta \\
\frac{E_{\rm des}}{R\,T^2}&= \frac{\nu}{\beta}\exp\!\Bigl(-\frac{E_{\rm des}}{R\,T}\Bigr) \\
\end{aligned}\]
$$
対数を取るとと以下の関係が得られる:
\[
2\ln T_{\rm max} - \ln \beta = \ln \frac{E_{\rm des}}{R \nu} + \frac{E_{\rm des}}{R\,T_{\rm max}}
\tag{★}
\]
Thieleモジュール
触媒が多孔質構造を持つとき、反応物は細孔内に拡散してから反応する。この時の触媒内部の反応物濃度を定量的に解析する。
細孔内の濃度について考える。
Show Code
import plotly.graph_objects as go
import numpy as np
# x 軸(相対距離)
x = np.linspace(0, 1, 200)
# スライダーに使う mL 値のリスト
mL_values = np.linspace(0.1, 10, 100)
# 初期値
mL_init = 2
C_init = np.exp(-mL_init * x)
C_avg_init = np.trapezoid(C_init, x)
# フィギュア作成
fig = go.Figure(
data=[
go.Scatter(x=x, y=C_init, mode='lines', name='Concentration Profile', line=dict(color='deepskyblue', width=3)),
go.Scatter(x=[0, 1], y=[C_avg_init, C_avg_init], mode='lines', name='Average', line=dict(color='deepskyblue', dash='dash'))
],
layout=go.Layout(
title='Concentration Profile in Catalyst Pore (Interactive mL)',
xaxis_title='x / L',
yaxis_title='C_A / C_AS',
template='plotly_white',
updatemenus=[{
"type": "buttons",
"buttons": [
{"label": "Play", "method": "animate", "args": [None, {"frame": {"duration": 50, "redraw": True}, "fromcurrent": True}]},
{"label": "Pause", "method": "animate", "args": [[None], {"frame": {"duration": 0, "redraw": False}, "mode": "immediate"}]}
]
}],
sliders=[{
"steps": [{
"args": [[f"{mL:.2f}"], {"frame": {"duration": 0, "redraw": True}, "mode": "immediate"}],
"label": f"{mL:.2f}",
"method": "animate"
} for mL in mL_values],
"currentvalue": {"prefix": "mL = "},
"pad": {"t": 50}
}]
)
)
# フレームの追加
fig.frames = [
go.Frame(
data=[
go.Scatter(x=x, y=np.exp(-mL * x)),
go.Scatter(x=[0, 1], y=[np.trapezoid(np.exp(-mL * x), x)] * 2)
],
name=f"{mL:.2f}"
) for mL in mL_values
]
fig.show()
ここで、微細な部分 \(\Delta x\) を考える。この部分では、
\[
\dv{N_A}{t}_{\text{in}} - \dv{N_A}{t}_{\text{out}} = \dv{N_A}{t}_{\text{rxn}}
\]
となる。ここで、左辺はフィックの拡散、右辺は表面における反応速度で、それぞれを式にして表すと次の通り。ただし単位は、単位長さあたりの変化率であることに注意。
\[
\dv{N_A}{t}_{\text{in}} = -D \pi r^2 \frac{\Delta C_A}{\Delta x}
\]
\[
\dv{N_A}{t}_{\text{out}} = -D \pi r^2 \frac{\Delta C_A'}{\Delta x}
\]
\[
\dv{N_A}{t}_{\text{rxn}} = - \frac{1}{S} \dv{N_A}{t} \times 2\pi r \Delta x = - k'' C_A \times 2\pi r \Delta x
\]
これらを代入すると、
\[
\begin{aligned}
- (D \pi r^2 \frac{\Delta C_A}{\Delta x} - D \pi r^2 \frac{\Delta C_A'}{\Delta x} ) &= - k'' C_A \times 2\pi r \Delta x \\
D \dv[2]{C_A}{x} &= k''' C_A
\end{aligned}
\]
となる。ここで反応速度定数は表面積ベースから体積ベースに変換した。これをこのままだと扱いにくいというか、個別個別で全部やるのが面倒くさいので、無次元化する。
\[
\begin{aligned}
C &= \frac{C_A}{C_{AS}} \\
\chi &= \frac{x}{L}
\end{aligned}
\]
とすると、
\[
\begin{aligned}
\dv[2]{C}{\chi} &= L^2\frac{k'''}{D} C = M_T^2 C
\end{aligned}
\]
となる。ここで、\(M_T\) はThieleモジュールと呼ばれる。
\[
M_T = L \sqrt{\frac{k'''}{D}}
\]
この微分方程式を解いて図解したのが上の図。具体的な \(k'''\) の中身については追いかけるのが面倒なので放置するが、その大きさによって律速がどっちなのかがわかる。
| \(\gg 1\) |
拡散律速 |
| \(\ll 1\) |
反応律速 |
次に、先ほどの微分方程式の解は、
\[
C = \frac{\cosh M_T(1 - \chi)}{\cosh M_T}
\]
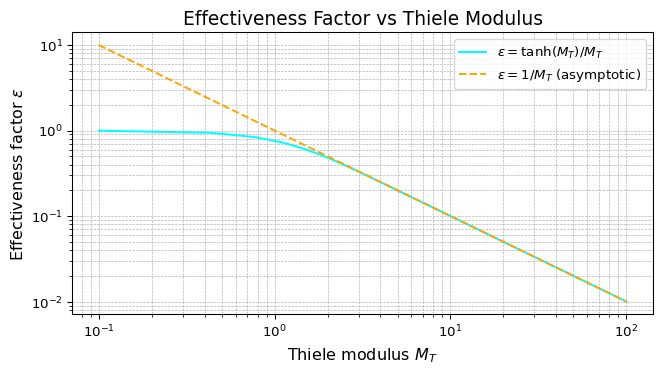
となる。で、この平均というのは
\[
\int_0^1 C \dd{\chi} = \frac{\tanh M_T}{M_T} = \mathscr{E}
\]
となって、これを有効性係数と呼んでいる。つまり、これが高ければ高いほど、反応率は高いというわけだ。これを式にまとめると、
\[
-r_A = k''' C_{AS} \mathscr{E}
\]
となる。
Show Code
import numpy as np
import matplotlib.pyplot as plt
# Thieleモジュールの範囲
M_T = np.linspace(0.1, 100, 300)
# 有効性係数 ε = tanh(M_T)/M_T
epsilon = np.tanh(M_T) / M_T
# プロット
fig, ax = plt.subplots(figsize=(7, 4))
ax.plot(M_T, epsilon, label=r'$\varepsilon = \tanh(M_T)/M_T$', color='cyan')
# 理想直線 ε = 1/M_T(拡散律速時の漸近直線)
ax.plot(M_T, 1 / M_T, '--', color='orange', label=r'$\varepsilon = 1/M_T$ (asymptotic)')
# 軸設定
ax.set_xscale('log')
ax.set_yscale('log')
ax.set_xlabel(r'Thiele modulus $M_T$', fontsize=12)
ax.set_ylabel(r'Effectiveness factor $\varepsilon$', fontsize=12)
ax.set_title('Effectiveness Factor vs Thiele Modulus', fontsize=14)
ax.grid(True, which="both", ls="--", linewidth=0.5)
ax.legend()
plt.tight_layout()
plt.show()
ここで、
\[
M_W = M_T^2 \mathscr{E} = \frac{L^2(-r_A)}{C_{AS} \mathscr{D}}
\]
というWeiszモジュールを導入する。これは分母が拡散速度のフィックの法則の式になっていて、分子が反応速度になっている。つまり、この式を見ることによって、拡散律速かどうかの実験チェックができる。
なぜこの式を使うかというと、この式の右辺は実験のみで計測が可能なところ。これによって \(M_T\) の評価なども可能である。