生産プロセス

University
2024
Author

Serika Yuzuki

Published

December 17, 2024

\[ \require{physics} \require{mhchem} \require{ams} \]

過去問まとめ

2023年度

問1

製錬：　鉱石中の化合物状態で存在している元素を、熱や化学的エネルギーを加えて金属状態にすること

精錬：　製錬で得られた金属から不純物を取り除き、純度を高める工程のこと

問2

略

問3

  1. 高炉挿入原料：鉄鉱石、コークス、石灰石

間接還元：

\[ \begin{aligned} \ce{3Fe2O3 + CO &-> 2Fe3O4 + CO2} \\ \ce{Fe3O4 + CO &-> 3FeO + CO2} \\ \ce{FeO + CO &-> Fe + CO2} \\ \end{aligned} \]

直接還元：

\[ \ce{FeO + C -> Fe + CO} \]

  • 水素還元は条件によって吸熱反応である。
  • コークスの通気性を保つ性質の代替が不可能。
  • 銑鉄化(浸炭)ができない。
  • 高炉に微粉化プラスチックを吹込み、熱分解で \(\ce{CO, H2}\) を発生し、還元剤・燃料としてコークスや微粉炭を代替する。
  • コークス炉で微粉化プラスチックを原料として利用しつつ、コークス使用量を削減する。

除冷スラグ：　自然放冷した結晶質のスラグ。空隙を含む岩石城で、道路やコンクリートに使われる。

水砕スラグ：　高温の溶融スラグを加圧水噴射急冷した非晶質のスラグ。気泡を含む粒子状。セメントの原料や路床材に使われる。

Show Code 
import numpy as np
import matplotlib.pyplot as plt
import math

# --- Vertices of ternary diagram ---
V_CaO = np.array([0.0, 0.0])
V_Al  = np.array([1.0, 0.0])
V_Si  = np.array([0.5, math.sqrt(3)/2])

def bary_to_xy(cao, al, si):
    s = cao + al + si
    cao, al, si = cao/s, al/s, si/s
    return cao*V_CaO + al*V_Al + si*V_Si

fig, ax = plt.subplots(figsize=(7, 6))

# --- Draw triangle ---
tri = np.vstack([V_CaO, V_Al, V_Si, V_CaO])
ax.plot(tri[:,0], tri[:,1], color="black")

# --- Axis ticks every 10% ---
ticks = np.linspace(0.1, 0.9, 9)

# SiO2 ticks (parallel to base)
for s in ticks:
    p1 = bary_to_xy(1-s, 0, s)
    p2 = bary_to_xy(0, 1-s, s)
    ax.plot([p1[0], p2[0]], [p1[1], p2[1]], color="lightgray", linewidth=0.8)
    ax.text(p2[0]+0.02, p2[1], f"{int(s*100)}%", fontsize=8, va="center")

# CaO ticks (parallel to Al2O3–SiO2 edge)
for c in ticks:
    p1 = bary_to_xy(c, 1-c, 0)
    p2 = bary_to_xy(c, 0, 1-c)
    ax.plot([p1[0], p2[0]], [p1[1], p2[1]], color="lightgray", linewidth=0.8)

# Al2O3 ticks (parallel to CaO–SiO2 edge)
for a in ticks:
    p1 = bary_to_xy(1-a, a, 0)
    p2 = bary_to_xy(0, a, 1-a)
    ax.plot([p1[0], p2[0]], [p1[1], p2[1]], color="lightgray", linewidth=0.8)

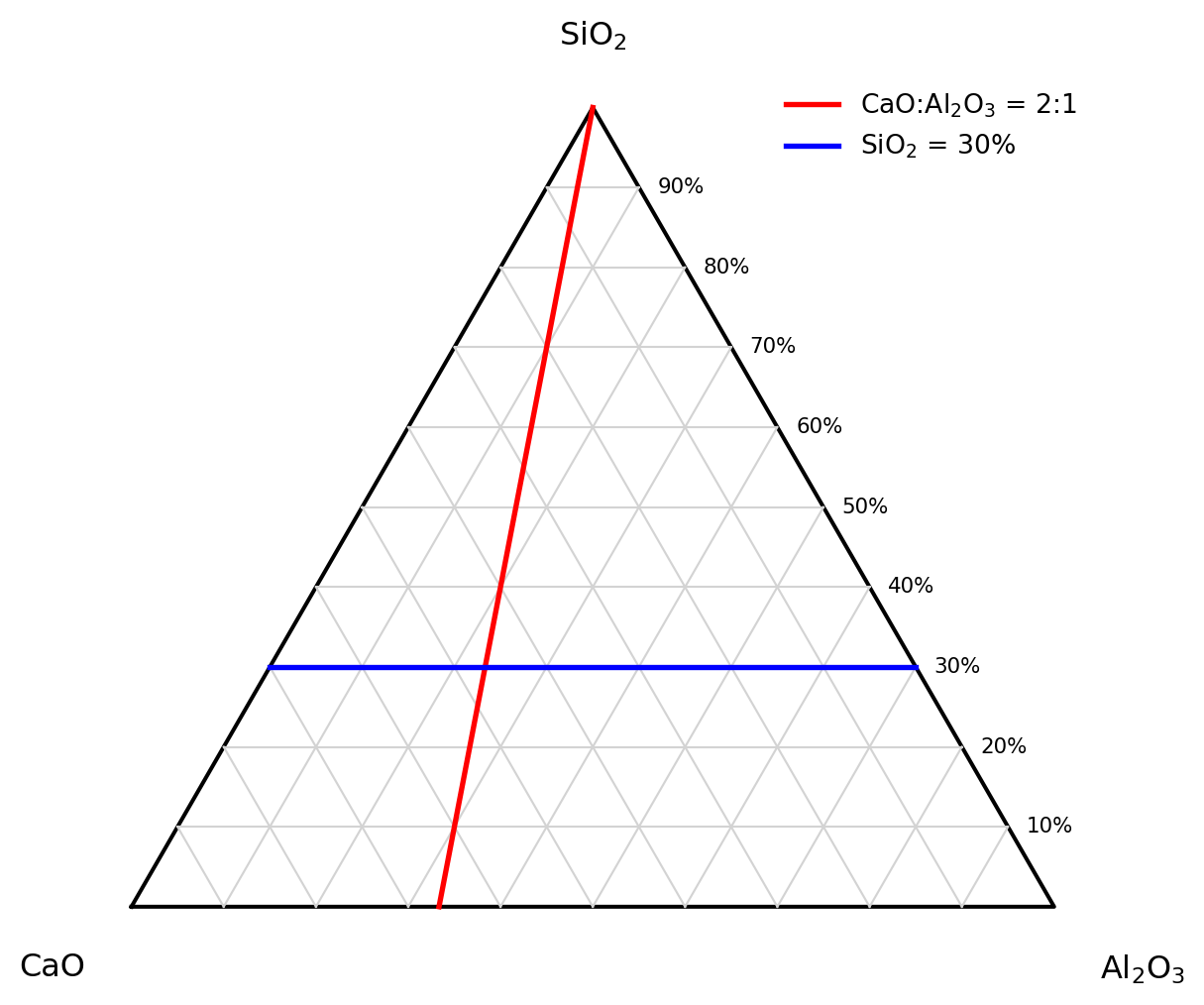
# --- Highlight required lines ---
# CaO : Al2O3 = 2 : 1
t = np.linspace(0, 1, 200)
cao = (2/3) * (1 - t)
al  = (1/3) * (1 - t)
si  = t
xy_ratio = np.vstack([bary_to_xy(cao[i], al[i], si[i]) for i in range(len(t))])
ax.plot(xy_ratio[:,0], xy_ratio[:,1], color="red", linewidth=2, label="CaO:Al$_2$O$_3$ = 2:1")

# SiO2 = 30%
p1 = bary_to_xy(0.70, 0.00, 0.30)
p2 = bary_to_xy(0.00, 0.70, 0.30)
ax.plot([p1[0], p2[0]], [p1[1], p2[1]], color="blue", linewidth=2, label="SiO$_2$ = 30%")

# --- Labels ---
ax.text(V_CaO[0]-0.05, V_CaO[1]-0.05, "CaO", ha="right", va="top", fontsize=12)
ax.text(V_Al[0]+0.05,  V_Al[1]-0.05,  "Al$_2$O$_3$", ha="left", va="top", fontsize=12)
ax.text(V_Si[0],       V_Si[1]+0.06,  "SiO$_2$", ha="center", va="bottom", fontsize=12)

ax.set_aspect("equal")
ax.axis("off")
ax.legend(loc="upper right", frameon=False)

plt.show()

3)4)

問4

\[ \ce{P + \frac{5}{4}O2 + \frac{3}{2}O^{2-} -> PO4^{3-}} \]

低温・高塩基性・高酸素分圧でリン酸イオンが安定。

定義式は次のとおり

\[ e_{\ce{P}}^{\ce{C}} = \lim _{ [\%1] \to 100} \pdv{\log_{10} f_{\ce{P}}}{[\%\ce{C}]} \]

実際の値は、

\[ \begin{aligned} \log_{10}f_{\ce{P}} &= e_{\ce{P}}^{\ce{C}} [\%\ce{C}] \\ &= 0.079 \times 4.5 \\ &= 0.3555 \\ \therefore \quad f_{\ce{P}} &= 10^{0.3555} = 2.27 \end{aligned} \]

\[ \begin{aligned} \Delta G_1^\circ &= -122200 - 19.25T\;(\mathrm{J/mol}) \\ \Delta G_1^\circ &= -RT\ln K_1 \\ \Rightarrow \ln K_1 &= -\frac{\Delta G_1^\circ}{RT} \\ &= \frac{122200+19.25T}{RT} \end{aligned} \]

\[ \begin{aligned} L_\ce{P} &= \frac{0.326 f_{\ce{P}} C_{\ce{PO4^{3-}}}p_{\ce{O2}}^{\frac{5}{4}}}{K_1} \\ &= \frac{0.326 \times 2.27 \times (10^{-15})^{\frac{5}{4}}}{\exp\qty(\frac{-(122200 + 19.25 \times 1573)}{8.314 \times 1573})} C_{\ce{PO4^{3-}}}\\ &= 1.14 \times 10^{-24} C_{\ce{PO4^{3-}}} \\ &= 5.00 \times 10^{2} \\ \therefore \quad C_{\ce{PO4^{3-}}} &= 4.40 \times 10^{26} \end{aligned} \]

Show Code 
import numpy as np
R = 8.314  # J/(mol·K)
T = 1573  # K
f_P = 2.27
p_O2 = 1e-15  # atm

delta_G1_0 = -122200 - 19.25 * T  # J/mol
K1 = np.exp(-delta_G1_0 / (R * T))
L_P = 5.00e2  # given
C_PO4_3_minus = L_P * K1 / (0.326 * f_P * p_O2**(5/4))
print("C_PO4^3- is:", C_PO4_3_minus, "mol/m^3")
C_PO4^3- is: 4.398695474423597e+26 mol/m^3

  1. 転炉精錬の主目的は、溶銑中の炭素を酸化反応によって除去し、所定の炭素量をもつ鋼を得ること。同時にSiやMnは優先的に酸化されスラグ中へ移行し、塩基性スラグと高い酸素ポテンシャル下でリンもリン酸塩として除去される。これらの処理を同時に実現し、外部加熱を用いずに溶鋼温度を上昇させることができる。

  • RD：アルゴンガスにの吹き込みによって真空槽に溶鉱を循環させる方法。H, N, COの除去に有効。
  • VD：真空槽内で溶鉱を攪拌し、真空引きによってHを効率的に除去する方法.

クロム酸化損失の抑制のために、AODやVODが用いられる。前者はアルゴンガスを吹き込んでCO分圧を下げる手法で、後者は真空下で酸素を吹き込むことでCOを吸い上げる手法。

問5

\(\ln p_{\ce{O2}}\) を表している。ある温度での縦軸の値から、反応が平衡となる酸素分圧を読み取れば良い。

傾きは \(-\Delta S\) であり、切片は \(\Delta H\) である。酸化反応でエントロピー変化が類似するため。

1600 Kでは \(\ce{SiO2}\) の生成Gibbsエネルギーが \(\ce{CO}\) の酸化反応より低く、\(\ce{SiO2}\) が熱力学的に安定であるため、 \(\ce{CO}\) による還元は困難である

問題

Back to top