\[ \require{physics} \require{mhchem} \require{ams} \]

過去問まとめ

2022年度

問1,2

理論

fccの間隙原子については、その原子が入り込む面で考えればいい。８面体は立方体の一面、４面体は斜め切りした時を考えればいい。

解答

八面体間隙の場合は、

\[ \begin{aligned} \sqrt{2} \times 2r_0 &= 2r + 2r_0 \\ r &= \qty(\sqrt{2}-1)r_0 \\ \end{aligned} \]

四面体間隙の場合は、

\[ \begin{aligned} 2r+2r_0 &= \frac{\sqrt{3}}{2} \times 2\sqrt{2}r \\ r &= \qty(\frac{\sqrt{6}}{2}-1)r_0 \\ \end{aligned} \]

問3

理論

正四面体を上下に重ねた時の高さを求めるだけ

解答

\[ 2\frac{\sqrt{6}}{3} \]

Show Code

import numpy as np

a = 2 * np.sqrt(6) / 3
print(a)

1.6329931618554518

問4

理論

ポーリングの法則についてまとめる。

番号	内容
1,2	\(r_c/r_a\) が安定の範囲にある
3	\(\text{結合強度}=\sum (\text{陽イオン原子価})/(\text{配位数})=\text{酸化物イオン原子価}\)
4	配位多面体の結合は隅から起こる

ペロブスカイト構造については次の図を参照

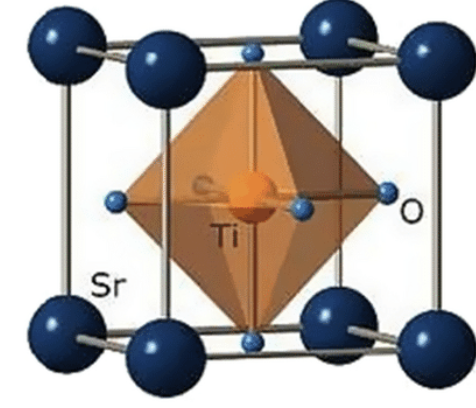
最後にイオン半径比の安定範囲についてまとめる。

配位数	安定範囲
4	0.225~0.414
6	0.414~0.732
8	0.732~1.0
12	1

解答

結合強度の計算は、

\[ \xi = \eval{\frac{3}{12} \times 4}_{\ce{Sr}} + \eval{\frac{3}{6} \times 2}_{\ce{Ti}} = 2 \]

となって、ポーリングの法則にしたがう。おそらくここまで書ければ点数がもらえるのではないかと思う。

次にイオン半径比は、

陽イオン	イオン比	安定範囲
\(\ce{Sr}\)	0.829	1
\(\ce{Ti}\)	0.52	0.414~0.723

Tiのイオン半径比は安定範囲にあるが、Srについては安定範囲にない。

ゴールドシュミットの許容因子という講義で出てきたものを使うと、

\[ t=\frac{ (r_{\ce{Sr}} + r_{\ce{O}}) }{ \sqrt{2}(r_{\ce{Ti}} + r_{\ce{O}}) }=0.87 \]

この計算だと、Srの半径が小さく不安定だと判定される。

問5

理論

何を答えればいいんだ……？　とりあえず講義で話してたことをまとめた。

解答

ガラスに含まれる理由：

非晶質であり、非化学両論的な組み合わせが可能
高い結合エネルギーによる安定性
豊富な資源

添加物の理由：

網目修飾体として、粘度や融点を調節するため
中間元素として、安定性を向上するため

問6

解答

\[ \ce{Y2O3 ->[ZrO2] 2Y_{Zr}^{'} + 3O_O^{\cross} + V_O^{..}} \]

\[ \ce{Y2O3 ->[ZrO2] 2Y_{i}^{...} + \frac{3}{2}O2(g) + 6e^{'}} \]

(b)の場合は反応後に酸素ガスが発生するため、酸素センサーなどを用いて実験すれば良い。

問7

理論

バイエルス応力と、イオン結合の話、滑り系の話でOKと思われる。

解答

パイエルス応力が大きい
イオン結合が崩れて電化的に不安定になったり、共有結合が切れたりするために、脆性が高い。金属は結合が非方向性で延性が高い。
構造が複雑で、独立した滑り系がない。
高温では滑り系が活動する。

問8

理論

CSLについての話。覚えればいい。

解答

CSL:隣接する結晶粒の格子構造が特定の割合で整合するような粒界

重要性:

機械特性的に強度や靭性、化学的に耐久性や耐腐食性を決定する。
電気、熱伝導性に対する障壁として働く。

問9

解答

①: 表面, ②: 圧粉体, ③: 粒界, ④: 体, ⑤: 密度, ⑥: オープンポア, ⑦: クローズポア, ⑧: 粒成長, ⑨: ポア, ⑩: 体, ⑪: 粒界

問10

解答

相変態：組織の変化により、物質の性質が変化させ、より強靭度の高い相に変化させる。
マイクロフラッキング：亀裂周りに微視割れが発生することにより微視割れによるプロセスゾーンを形成し、応力集中を緩和して、破壊靭性を見かけ上向上させる
亀裂の偏向：亀裂に変更を生じさせ、亀裂進展のエネルギー解放率が増加するため、亀裂進行抵抗の増加につながる。
引き抜け：割れ進展時に繊維が引き抜かれることでエネルギーを吸収し、破壊抵抗を高める
架橋：繊維や粒子が亀裂面間を架橋して亀裂進展抵抗が増大する。
残留応力：初期き裂が発生しても残留応力によりき裂に圧縮がかかるため、より大きな外部からの応力が必要となる。

問11

理論

講義で出てきたっけ……？　記憶にありません。

解答

安定き裂進展時におけるき裂進展量と破壊抵抗値との関係を示す曲線。亀裂進展が始まる初期段階では破壊抵抗が低く、亀裂が進展するにつれて破壊抵抗が増加する場合が多いのが特徴。

問12

解答

積層コンデンサー：積層構造のセラミックスを用いたコンデンサで、高誘電率材料により高い静電容量を実現。小型・高容量で電子機器に広く使用される。主にチタン酸バリウムが使われる。

圧電セラミックス：機械的変形により電圧を発生させる特性を持つセラミックス。逆に電圧で変形も可能。高感度や精密な制御が求められる用途に適していて、センサー、アクチュエーター、超音波機器などで活用される。

バリスター：電圧が一定値を超えると急激に電気抵抗が下がる非線形抵抗素子。酸化亜鉛が主材料。耐久性や迅速な応答性が重要な電源回路の過電圧保護や雷サージ対策に用いられる。

問13

解答

固溶体の焼結の結果粒界ができることで、相転移点以上で電子が界面準位に捕獲されるショットキー障壁が形成されることで電気抵抗が急激に増加する。

問14

理論

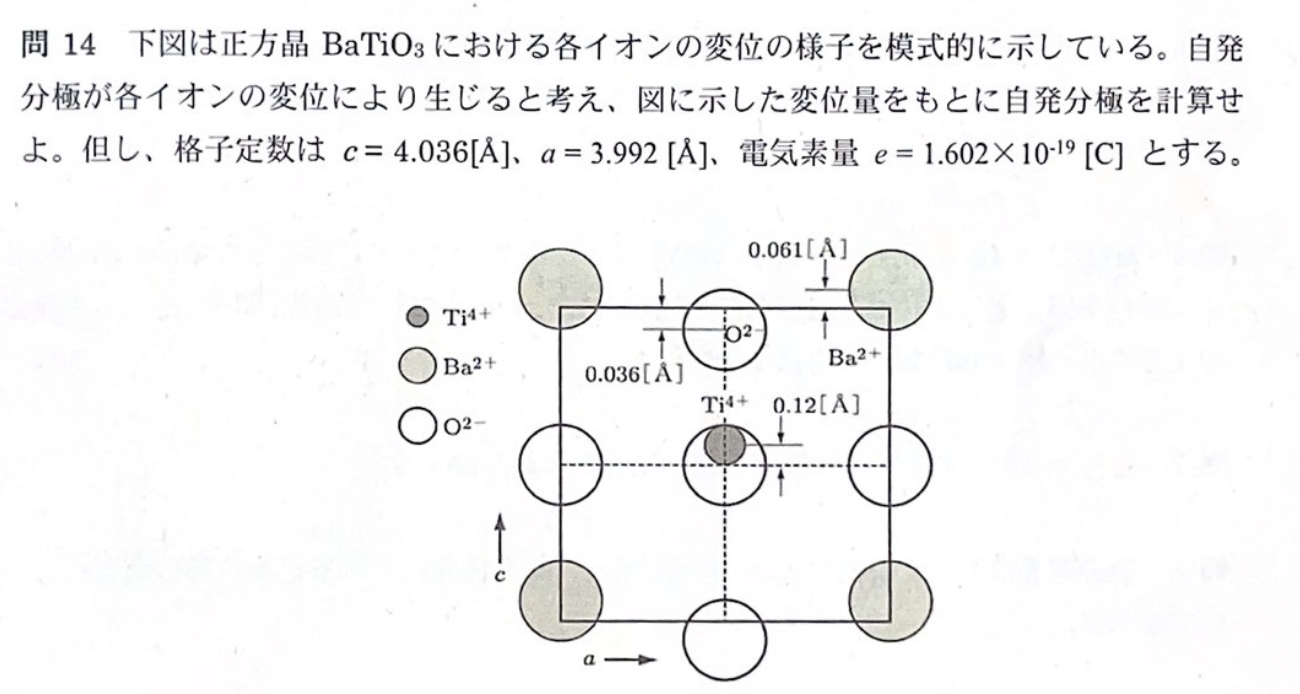
分極モーメントは

\[ \mathbfit{\mu} = q \times \Delta \mathbfit{r} \]

で表される。ここで、\(\Delta \mathbfit{r}\) はずれた距離である。そして、分極 ionic polarizability は

\[ \mathbfit{P} = N \times \mathbfit{\mu} = \frac{\mathbfit{\mu}_{\text{格子内}}}{V_\text{単位体積}} \]

で表される。ここで、\(N\) は単位体積あたりの双極子数である。

この問題ではまず格子内の分極モーメントを求め、次に単位体積で割れば良い。格子自体の体積については、\(V = a^2c\) で求められる。 \(a^2\) は基準にした酸素イオンの間隔で、対称性から考えればわかる。

解答

上向を正とする。

\[ \begin{aligned} \mu = e ( &\eval{\qty{{1_{\text{個}} \times (+4)_{\text{価数}} \times 0.12 [Å]}}}_{\ce{Ti^{4+}}} + \\ &\eval{\qty{{1_{\text{個}} \times (-2)_{\text{価数}} \times -0.036 [Å]}}}_{\ce{O^{2-}}} + \\ &\eval{\qty{{1_{\text{個}} \times (+2)_{\text{価数}} \times 0.061 [Å]}}}_{\ce{Ba^{2+}}} ) \\ &= 1.080 \times 10^{-29} \, \mathrm{C} \cdot \mathrm{m} \\ P &= \frac{\mu}{V} = 1.679 \times 10^{-1} \, \mathrm{C} \cdot \mathrm{m}^{-2} \end{aligned} \]

Show Code

import numpy as np

e = 1.602e-19
a = 3.992e-10
c = 4.036e-10

mu = e * (1 * 4 * 0.12e-10 + 1 * (-2) * (-0.036e-10) + 1 * 2 * 0.061e-10)
V = a**2 * c
P = mu / V

print("mu is: ", mu, "\nP is: ", P)

mu is:  1.0797479999999999e-29 
P is:  0.1678766079680568

問15

解答

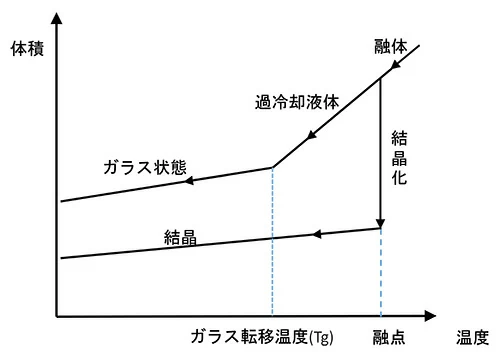
ガラスになる物質を高温からゆっくり冷却すると結晶化するが、急冷すると粘性が増大し融点でも結晶化せず過冷却され、その体積は滑らかに減少し、ガラス転移点に達すと体積変化が急に小さくなる。 \(T_g\) はガラスを特徴づける最も基本的な物性値で、冷却速度が遅い場合は網目が連続的につながっている構造を持ち、その値は高く、冷却速度が速い場合は網目が不連続になって低くなる。

問16

解答

熱伝導率を \(\kappa\) とすると、キャリアの比熱を \(c\) 、音速を \(c\) 、平均自由行程を \(l\) とすると、熱伝導率は

\[ \kappa = \frac{1}{3} cvl \]

と示されている。キャリアの比熱と速度は固体内では変わらないので、 \(l\) が熱伝導率に影響を与える。

ここで、ガラス内部の構造は結晶内部に比べて複雑であり、ある２点の原子A,Bを通る経路同士でキャリアの位相が干渉してしまうため、平均自由行程が短くなる。そのため、熱伝導率が低くなる。

問17

解答

XRD, EDS, IRなどの方法によって使用されている素材の組成を調べることによって、適当な現代の材料を選定する。次に、高精度な焼結技術を用いて、異なる材料、釉薬、焼成条件を変化させながら試作を繰り返し、最適な条件を見つけ出すことが求められる。

その他

2023-1

理論

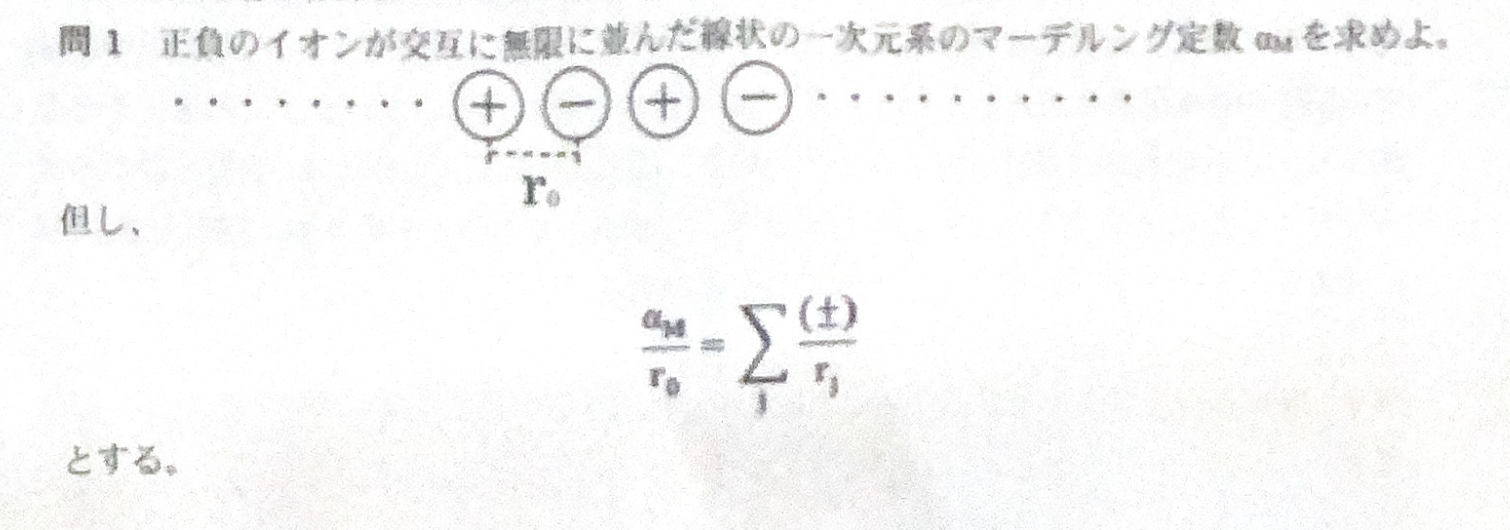
ポテンシャルの話。

\[ \ln(1+x) = x - \frac{x^2}{2} + \frac{x^3}{3} - \cdots \]

解答

\[ V = - \frac{e^2}{4\pi \varepsilon_0 r_0} \times 2 \qty(1 - \frac{1}{2} + \frac{1}{3} - \cdots)= - \frac{e^2}{4\pi \varepsilon_0 r_0} 2\ln 2 \]

以上より \(2\ln 2\) となる。