固体物性学

\[ \require{physics} \require{mhchem} \]

ノート

結晶格子

結晶とは

• 結晶とは、原子や分子が規則的に並んだ固体のことである。
• 理想的な結晶、現実の結晶、多結晶、非晶質(アモルファス)の4つの種類がある。

講義ではまず２次元Latticeについて考える。

基本単位胞

• 結晶構造を記述するための基本単位胞とは、結晶構造の最小単位であり、その結晶構造を無限に繰り返すことで全体の結晶構造が構築される。
• 基本単位胞の取り方は無限にあるが、最も簡単なものを選ぶといいらしい。
• 基本単位胞内の任意の点を格子点と呼んでいる。ただし、全ての別の単位胞に対して同じ位置として考える。バラバラに選ぶものではない。
• 格子点同士を最短で結ぶベクトルを基本並進ベクトルと呼ぶ。

import matplotlib.pyplot as plt
import numpy as np

# Define the lattice vectors
a1 = np.array([1, 0])
a2 = np.array([0, 1])

# Generate a grid of lattice points
x = np.arange(-2, 3)
y = np.arange(-2, 3)
X, Y = np.meshgrid(x, y)

# Plot the lattice points
plt.figure(figsize=(6, 6))
plt.scatter(X, Y, color='blue')

# Plot the lattice vectors
plt.quiver(0, 0, a1[0], a1[1], angles='xy', scale_units='xy', scale=1, color='red')
plt.quiver(0, 0, a2[0], a2[1], angles='xy', scale_units='xy', scale=1, color='green')

# Set the aspect ratio and limits
plt.gca().set_aspect('equal', adjustable='box')
plt.xlim(-2.5, 2.5)
plt.ylim(-2.5, 2.5)

# Add labels
plt.text(a1[0], a1[1], 'a1', fontsize=12, ha='right')
plt.text(a2[0], a2[1], 'a2', fontsize=12, va='bottom')

plt.show()

• すると、任意の格子点は \(\symbfit{R} = n_1 \symbfit{a}_1 + n_2 \symbfit{a}_2\) と表すことができる。

３次元結晶格子

３次元結晶格子は、２次元結晶格子の拡張である。並進ベクトルの性質はそれほど変わらない。３次元格子は１４種類のブラベ格子に分類される。並進ベクトルを基底ベクトルで表すなんてこともする。 - 体心立方格子 \[ \begin{aligned} \symbfit{a}_1 &= \frac{a}{2} ( \symbfit{e}_x + \symbfit{e}_y + \symbfit{e}_z ) \\ \symbfit{a}_2 &= \frac{a}{2} ( -\symbfit{e}_x + \symbfit{e}_y + \symbfit{e}_z ) \\ \symbfit{a}_3 &= \frac{a}{2} ( \symbfit{e}_x - \symbfit{e}_y + \symbfit{e}_z ) \\ \end{aligned} \]

• 面心立方格子 \[ \begin{aligned} \symbfit{a}_1 &= \frac{a}{2} ( \symbfit{e}_x + \symbfit{e}_y ) \\ \symbfit{a}_2 &= \frac{a}{2} ( \symbfit{e}_y + \symbfit{e}_z ) \\ \symbfit{a}_3 &= \frac{a}{2} ( \symbfit{e}_z + \symbfit{e}_x ) \\ \end{aligned} \]

• 基本単位胞では面倒なことがあるので、慣用単位砲で考えることもある。その一例として、ウィグナー・ツァイト胞がある。ウィグナーサイツ胞とは、ある格子点と、その周りの格子点との間の垂直二等分面で囲まれた領域における最小のセル（胞）のことである。

import matplotlib.pyplot as plt
import numpy as np
from matplotlib.patches import Rectangle

# Define the lattice vectors
a1 = np.array([1, 0])
a2 = np.array([0, 1])

# Generate a grid of lattice points
x = np.arange(-2, 3)
y = np.arange(-2, 3)
X, Y = np.meshgrid(x, y)

# Plot the lattice points
plt.figure(figsize=(6, 6))
plt.scatter(X, Y, color='blue')

# Plot the lattice vectors
plt.quiver(0, 0, a1[0], a1[1], angles='xy', scale_units='xy', scale=1, color='red')
plt.quiver(0, 0, a2[0], a2[1], angles='xy', scale_units='xy', scale=1, color='green')

# Draw the Wigner-Seitz cell
rectangle = Rectangle((-0.5, -0.5), 1, 1, edgecolor='black', facecolor='none')
plt.gca().add_patch(rectangle)

# Set the aspect ratio and limits
plt.gca().set_aspect('equal', adjustable='box')
plt.xlim(-2.5, 2.5)
plt.ylim(-2.5, 2.5)

# Add labels
plt.text(a1[0], a1[1], 'a1', fontsize=12, ha='right')
plt.text(a2[0], a2[1], 'a2', fontsize=12, va='bottom')

plt.show()

import matplotlib.pyplot as plt
import numpy as np
from matplotlib.patches import RegularPolygon

# Define the lattice vectors
a1 = np.array([1, 0])
a2 = np.array([1/2, np.sqrt(3)/2])

# Generate a grid of lattice points
x = np.arange(-2, 3)
y = np.arange(-2, 3)
X, Y = np.meshgrid(x, y)

# Generate the hexagonal lattice points
X_hex = X + Y/2
Y_hex = Y * np.sqrt(3)/2

# Plot the lattice points
plt.figure(figsize=(6, 6))
plt.scatter(X_hex, Y_hex, color='blue')

# Plot the lattice vectors
plt.quiver(0, 0, a1[0], a1[1], angles='xy', scale_units='xy', scale=1, color='red')
plt.quiver(0, 0, a2[0], a2[1], angles='xy', scale_units='xy', scale=1, color='green')

# Draw the Wigner-Seitz cell
polygon = RegularPolygon((0, 0), 6, radius=1/np.sqrt(3), edgecolor='black', facecolor='none')
plt.gca().add_patch(polygon)

# Set the aspect ratio and limits
plt.gca().set_aspect('equal', adjustable='box')
plt.xlim(-2.5, 2.5)
plt.ylim(-2.5, 2.5)

# Add labels
plt.text(a1[0], a1[1], 'a1', fontsize=12, ha='right')
plt.text(a2[0], a2[1], 'a2', fontsize=12, va='bottom')

plt.show()

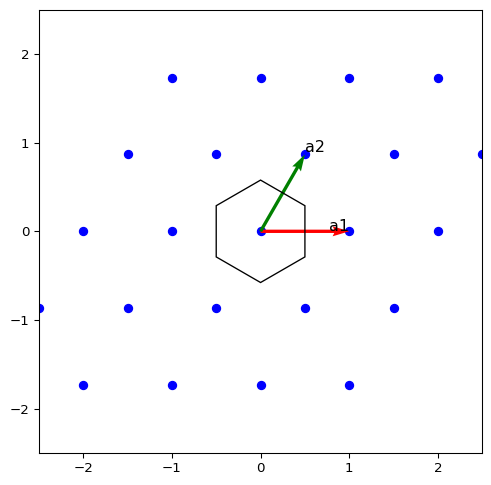
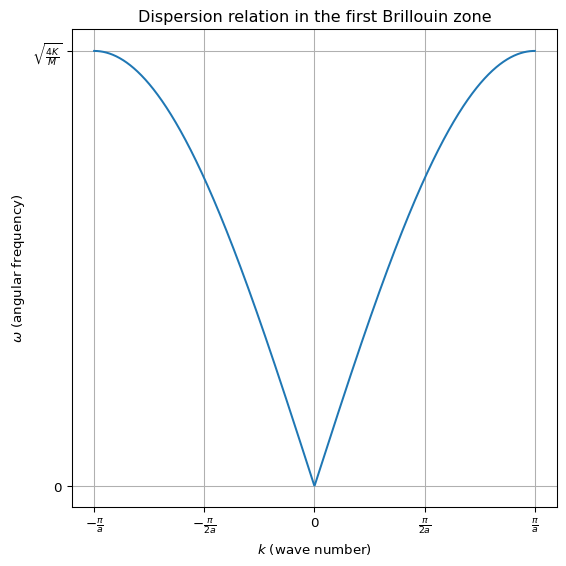
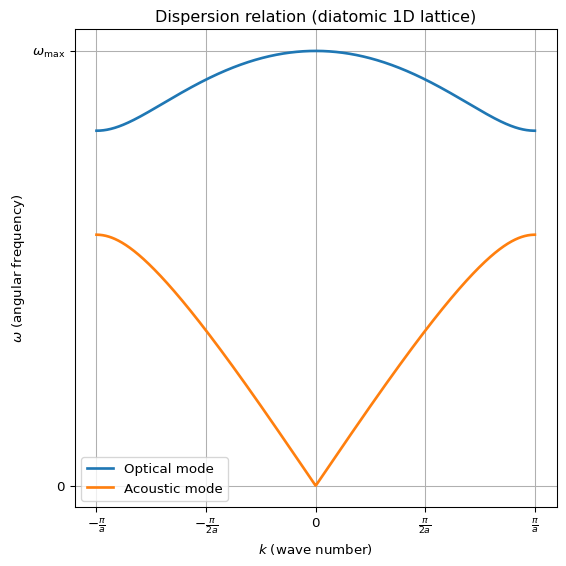
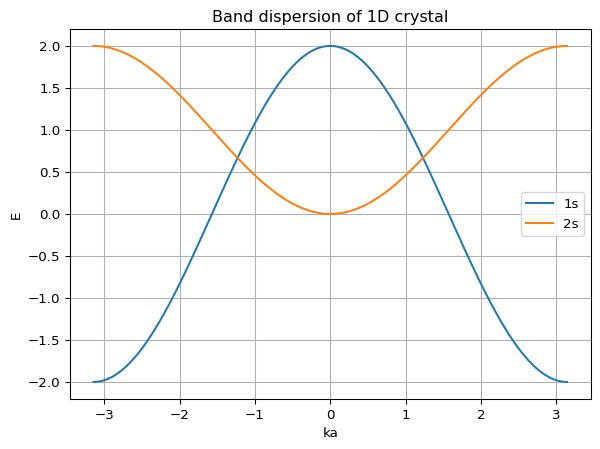
逆格子

周期性のある関数を一つ考える。

\[ f(x) = f(x+n\lambda) \]

この時、

\[ f(x)=\sum_{n=-\infty}^{\infty} c_n \exp \left(\frac{2 \pi i n x}{\lambda}\right) = \sum_{n=-\infty}^{\infty} c_n \exp \left(iG_n x\right) \]

ただしフーリエ係数は, \[ c_n=\frac{1}{\lambda} \int_0^\lambda f(x) \exp \left(-iG_n x\right) \dd x \]

ここで、 \(G_n = 2\pi n / \lambda\) となり、離散的な値を持つ。この時の \((G_n)\) を逆格子ベクトルと呼ぶ。逆格子スペクトルは、要するに \(G_n\) を横軸にして、どの端数が一番強く現れているのかを、 \(c_n\) 高さで表しているだけなのだ。

これを立体に拡張させる。

\[ f(\symbfit{X})=\sum_{n=-\infty}^{\infty} c_n \exp \left(i\symbfit{G_n} \cdot (\symbfit{r}+\symbfit{R})\right) \]

ここで、 \(\symbfit{R}\) は関数が一周して帰ってくる値。

\[ \symbfit{G_n} \cdot \symbfit{R} = 2\pi N \]

というのは次からわかる。

\[ \begin{aligned} \symbfit{G_n} \cdot \symbfit{a}_1 &= 2\pi n_1 \\ \symbfit{G_n} \cdot \symbfit{a}_2 &= 2\pi n_2 \\ \symbfit{G_n} \cdot \symbfit{a}_3 &= 2\pi n_3 \\ \end{aligned} \]

この理由は、要するに波が一周して戻るから。数式で表せば、\(f(\symbfit{r}+\symbfit{R})=(\symbfit{r})\) で導ける。

ここで次のようなベクトルを考える。

\[ \symbfit{G_n} = n_1 \symbfit{b}_1 + n_2 \symbfit{b}_2 + n_3 \symbfit{b}_3 \]

これで、

\[ \symbfit{a_i} \cdot \symbfit{b}_j = 2\pi \delta_{ij} \]

とすれば、

\[ \symbfit{G_n} \cdot \symbfit{a_i} = 2\pi n_i \]

になる。これを逆格子ベクトルと呼ぶ。

\[ \begin{aligned} \symbfit{b}_1 &= 2\pi \frac{\symbfit{a}_2 \times \symbfit{a}_3}{\symbfit{a}_1 \cdot (\symbfit{a}_2 \times \symbfit{a}_3)} \\ \symbfit{b}_2 &= 2\pi \frac{\symbfit{a}_3 \times \symbfit{a}_1}{\symbfit{a}_2 \cdot (\symbfit{a}_3 \times \symbfit{a}_1)} \\ \symbfit{b}_3 &= 2\pi \frac{\symbfit{a}_1 \times \symbfit{a}_2}{\symbfit{a}_3 \cdot (\symbfit{a}_1 \times \symbfit{a}_2)} \\ \end{aligned} \]

となる。これが何がありがたいかというと、空間内の任意の周期性のある物理量をフーリエ変換することで、逆格子空間における格子点の位置に一つ一つ何かしらの強さの値を置くことで見ることができることかもしれない。つまり、フーリエ変換の長さが短くなるほどに、それを表すのに必要な逆空間の格子点は減るということかな？　ここら辺が何の役に立つのかわからんのは、後からわかる感じの説明の仕方をしてるから。

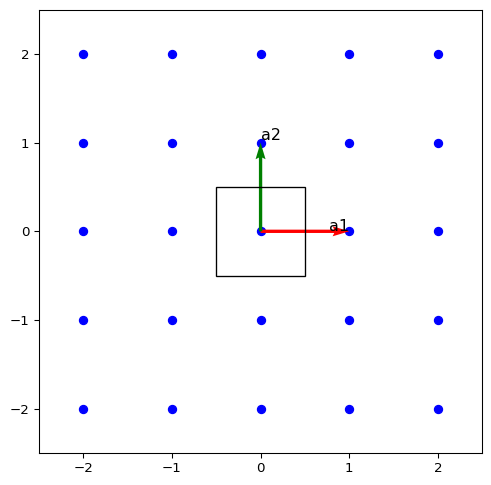
例として二次元単純結晶について考えると、

\[ \begin{aligned} \symbfit{a}_1 &= a \symbfit{e}_x \\ \symbfit{a}_2 &= b \symbfit{e}_y \\ \end{aligned} \]

これの逆格子ベクトルは、

\[ \begin{aligned} \symbfit{b}_1 &= \frac{2\pi}{a} \symbfit{e}_y \\ \symbfit{b}_2 &= \frac{2\pi}{b} \symbfit{e}_x \\ \end{aligned} \]

なので、

\[ \begin{aligned} k_x \in \left[ -\frac{\pi}{a}, \frac{\pi}{a} \right] \\ k_y \in \left[ -\frac{\pi}{b}, \frac{\pi}{b} \right] \\ \end{aligned} \]

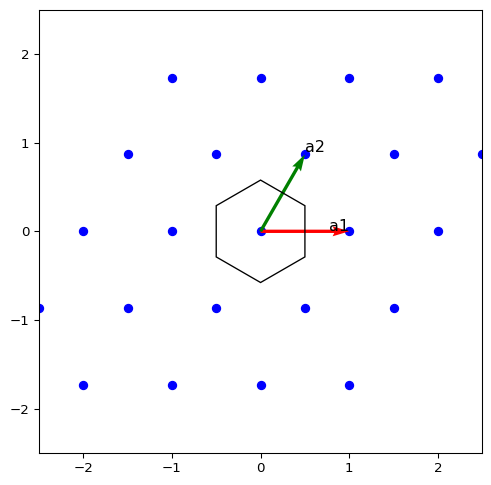
がBrillouin Zoneとなる。つまり、逆空間内のWigner-Seitz cellになる。

ブリルアンゾーン

一次元の場合、結晶間隔を \(a\) とすると、

\[ -\frac{\pi}{a} \leq k \leq \frac{\pi}{a} \]

これをブリルアンゾーンと呼ぶ。これは逆格子ベクトルの範囲を表している。これも何でやってるかはわからん。

結晶によるX線回折

この話は先ほどの議論とは類似はするが話が違う気がする。

考えを乱さないためにここには書かないし、教科書に板書がそのままある。

ちょっとした話だが、要するに、ラウエ関数

\[ \frac{\sin ^2 \left(\pi N \symbfit{r}\cdot \symbfit{K}_x \right)}{\sin ^2 \left(\pi \symbfit{r}\cdot \symbfit{K}_x \right)} \]

を考えた時に、 \(N\) というのは、どれだけ原子数をスキップしてX線が強め合うのかで、このグラフは \(\symbfit{a}\cdot \symbfit{K}_x\) が整数の時に最強になって、ゆえにそれをラウエ条件と呼んでいて、

\[ \begin{aligned} \symbfit{r}\cdot \symbfit{K}_x = h \\ \symbfit{r}\cdot \symbfit{K}_y = k \\ \symbfit{r}\cdot \symbfit{K}_z = l \\ \end{aligned} \]

とかってなって、上と途中と同じ理屈でやってるだけで、議論は最初から同じではない。

X線回折になると、単位胞子の中身だけを考えれば、その原子分子の位置がわかるということになる。だから、ブリルアンゾーンの中だけを考えれば、波長のより短いところにあるというふうに見れる場所の原子の場所がわかる。それ以上の波長の場所にあるのは、つまり、繰り返されたものだけだと言える。

結合

結合エネルギーとは、結晶を引き剥がして無限遠に持っていくのに必要なエネルギー。

共有結合

水素の原子軌道を考える。

\[ \hat{H} = -\frac{\hbar^2}{2me} \nabla - \frac{e^2}{4\pi\epsilon_0 r_1} - \frac{e^2}{4\pi\epsilon_0 r_2} + \frac{e^2}{4\pi\epsilon_0 R} \]

この軌道方程式を解く。式がかなり面倒なので、次のような前提で解くことになる。

• \(\phi\) は二つの波動関数 \(\phi_1\) と \(\phi_2\) の線形結合で表せる
• \(\phi_1\) と \(\phi_2\) はそれぞれ、二つの陽子が片方だけ存在する時に表される電子の波動関数である

これがLCAO法と呼ばれる。

\[ \hat{H} (c_1\phi_1 + c_2\phi_2) = E(c_1\phi_1 + c_2\phi_2) \]

左から \(\phi_1^*\) とかけて積分すると

\[ \begin{aligned} H_{11} c_1 + H_{12} c_2 &= Ec_1 + S_{12}Ec_2 \\ H_{21} c_1 + H_{22} c_2 &= S_{21}Ec_1 + Ec_2 \\ \end{aligned} \]

これを整理すると、

\[ \begin{pmatrix} H_{11} - E & H_{12} - S_{12} \\ H_{21} S_{21} & H_{22} - E \\ \end{pmatrix} \begin{pmatrix} c_1 \\ c_2 \\ \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\ \end{pmatrix} \]

この非自明な解があるのは、行列式がゼロになる時である。

\[ \begin{vmatrix} H_{11} - E & H_{12} -ES_{12} \\ H_{21}- ES_{21} & H_{22} - E \\ \end{vmatrix} = 0 \]

\(S_{12} = S_{21}, H_{12}=H_{21}, H_{11}=H_{22}\) であることを考えると、

\[ (H_{11} - E)^2 - (H_{12} - SE) = 0 \]

となって以下の解が出てくる

\[ \begin{aligned} E_+ = \frac{H_{11} + H_{12}}{1+S} \\ E_- = \frac{H_{11} - H_{12}}{1-S} \\ \phi_+ = \frac{\phi_1 + \phi_2}{\sqrt{2(1+S)}} \\ \phi_- = \frac{\phi_1 - \phi_2}{\sqrt{2(1-S)}} \\ \end{aligned} \]

ダイヤモンドの共有結合

\[ \begin{aligned} \phi_1 &= \frac{1}{2} (\xi_{2s} - \xi_{2p_x} - \xi_{2p_y} - \xi_{2p_z}) \\ \phi_2 &= \frac{1}{2} (\xi_{2s} 2 \xi_{2p_x} + \xi_{2p_y} + \xi_{2p_z}) \\ \phi_3 &= \frac{1}{2} (\xi_{2s} + \xi_{2p_x} - \xi_{2p_y} - \xi_{2p_z}) \\ \phi_4 &= \frac{1}{2} (\xi_{2s} - \xi_{2p_x} + \xi_{2p_y} - \xi_{2p_z}) \\ \end{aligned} \]

ところが、\(sp3\) 混成軌道への昇位にかかるエネルギーは \(7.4 \symup{eV}\) もかかるが、結合エネルギーが \(7.3 \symup{eV}\) もあるので、安定している。

イオン結合

\(i\) 番目のイオンにかかるイオン間のクーロン相互作用によるエネルギーは

\[ \begin{aligned} E_i &= -\frac{e^2}{4\pi\epsilon_0} \sum_{j \neq i} \frac{Z_i Z_j}{r_{ij}}\\ &= M \times \frac{Z_i Z_j e^2}{4 \pi \epsilon d} \end{aligned} \]

ここで \(M\) はマーデルング定数という。

自由電子論

箱型ポテンシャルの復習

箱型ポテンシャルの中にある電子のエネルギー分布を考える。

\[ \begin{aligned} \psi_{\symbfit{k}}(\symbfit{r}) &= \frac{1}{\sqrt{V}} \exp(i \symbfit{k} \cdot \symbfit{r}) \\ E_{\symbfit{k}} &= \frac{\hbar^2 k^2}{2m} \\ \symbfit{k} &= \frac{2\pi}{L} (n_x, n_y, n_z) \end{aligned} \]

ここら辺は復習。忘れたら、

\[ \begin{aligned} \hat{H}\psi_{\symbfit{k}}(\symbfit{r}) &= E_{\symbfit{k}} \psi_{\symbfit{k}}(\symbfit{r}) \\ -\frac{\hbar^2}{2m} \nabla^2 \psi_{\symbfit{k}}(\symbfit{r}) &= E_{\symbfit{k}} \psi_{\symbfit{k}}(\symbfit{r}) \\ \end{aligned} \]

これを変数分離で解けばいい。

状態密度・フェルミエネルギー

波数 \(\symbfit{k}\) が　\(k_i = \frac{2\pi}{L} n_i\) であることを考えた時、要するに \((2\pi/L)^3\) ごとに一個の状態があるから、体積あたりの状態数は \(1/(2\pi/L)^3\) になる。

次に、状態密度 \(D(E)\) を導入する。こいつは、エネルギー \(E\) の時の状態の数 \(N\) の \(E\) 微分だ。別の分野だと数を時間で微分してその増減を見たりするんだが、こいつは数をエネルギーで微分して、その増減を見てるわけ。

\(D(E)\dd E\) ってのは \(E \sim E+\dd E\) の間にある状態の数の密度ってわけで、 \(E\) の状態下での波数 \(k\) の球の体積を考えて、電子スピンの自由度2をかけてやって

\[ D(E)\dd E = 2 \times 4\pi k^2 \dd k \times \frac{1}{(2\pi/L)^3} \]

ここで、

\[ \dd k = \frac{1}{2} \sqrt{\frac{2m_e}{\hbar^2E}} \dd E \]

だから、状態密度ってのは、

\[ D(E) = \frac{L^3}{2\pi^2} \left( \frac{2m_e}{\hbar^2} \right)^{3/2} \sqrt{E} \]

となる。

フェルミエネルギーってのは、ある状態の数 \(N\) になるようなエネルギーのことだから、

\[ \begin{aligned} \int _0^{E_F} D(E) \dd E &\triangleq N \\ E_F &= \frac{\hbar^2}{2m_e} \left( \frac{3\pi^2 N}{L^3} \right)^{2/3} \\ \end{aligned} \]

今までのはめんどくさい方の考え方。別の導き方で考える。

要するに \(N\) ってのは、 \(\symbfit{k}\) の空間の球体体積を考えればいい。球体内の状態の数なんだから、体積あたりの状態数と電子スピンの自由度2をかけてやればいい。

\[ \begin{aligned} N(E) &= 2 \frac{4\pi}{3} k^3 \frac{L^3}{(2\pi)^3} = \frac{V}{3\pi^2} \qty(\frac{2m_eE}{\hbar^2})^{3/2} \\ D(E) &= \frac{dN}{dE} = \frac{L^3}{2\pi^2} \left( \frac{2m_e}{\hbar^2} \right)^{3/2} \sqrt{E} \\ \end{aligned} \]

バンド理論

詳しくは教科書 矢口裕之 (2017) を参照。ここでは大まかに理論を追うだけにする。

まず、ブロッホの定理。これは、繰り返し単位がある結晶内での波動関数が、

\[ \psi_{\symbfit{k}}(\symbfit{r} + \symbfit{R}) = \psi_{\symbfit{k}}(\symbfit{r}) \exp(i \symbfit{k} \cdot \symbfit{R}) \]

と表せるという定理。つまりは、繰り返し単位が存在するって話。

次に、そんな繰り返し単位がある結晶内での波動関数というのは、繰り返し単位である基本単位胞の位置からくる位置ベクトル \(\symbfit{R}_n\) と、その単位胞内に存在する原子による位置ベクトル \(\symbfit{r}_j\) を用いて、

\[ \phi(\symbfit{r}) = \sum_{\symbfit{R}_n} \sum_j \sum_\mu c_{j \mu} \exp \qty{i \symbfit{k}\cdot (\symbfit{R}_n + \symbfit{r}_j)} \phi_{j \mu}(\symbfit{r} - \symbfit{R}_n - \symbfit{r}_j) \]

と表せる。ここで \(\mu\) は原子の軌道関数の指定に使われる。例えば \(1s, \ 2s, \ 2p_x, \ 2p_y, \ 2p_z\) など。つまり、 \(n\) 個目の単位胞の \(j\) 番目の原子の \(\mu\) 番目の軌道関数による波動関数を \(\phi_{j \mu}(\symbfit{r} - \symbfit{R}_n - \symbfit{r}_j)\) として、それぞれの軌道関数による波動関数を \(c_{j \mu}\) の重みをつけて、線型結合で表しているだけ。

これが満たすべき波動方程式は、

\[ \hat{H} \phi(\symbfit{r}) - E \phi(\symbfit{r}) = 0 \]

これを左辺から \(\exp \qty{ - i \symbfit{k}\cdot (\symbfit{R}_n + \symbfit{r}_j)} \phi_{j \mu}^{\ast}(\symbfit{r} - \symbfit{R}_{n'} - \symbfit{r}_{j'})\) とかけて解析をしていく。

\[ \sum_{\symbfit{R}_n} \sum_j \sum_\mu c_{j \mu} \exp \qty{i \symbfit{k}\cdot (\symbfit{R}_n + \symbfit{r}_j - \symbfit{R}_{n'} - \symbfit{r}_{j'})} \qty( \bra{n'j'\mu'} \hat{H} \ket{n j \mu} - E \bra{n'j'\mu'} \ket{n j \mu} ) = 0 \]

これで、色々とモデル化をして考えていくわけだ。その具体例については、過去問に掲載する。

過去問

2018年度

問1

結晶格子と逆格子について、以下の問いに答えよ。

(a)

2次元単純直方格子（a ≠ b）と2次元六方格子のそれぞれについて、格子点と基本並進ベクトルを図示せよ。また、それらの図にウィグナー・ザイツ胞を書き入れよ。

理論

ウィグナーサイツ胞とは、ある格子点と、その周りの格子点との間の垂直二等分面で囲まれた領域における最小のセル（胞）のことである。

解答

import matplotlib.pyplot as plt
import numpy as np
from matplotlib.patches import Rectangle

# Define the lattice vectors
a1 = np.array([1, 0])
a2 = np.array([0, 1])

# Generate a grid of lattice points
x = np.arange(-2, 3)
y = np.arange(-2, 3)
X, Y = np.meshgrid(x, y)

# Plot the lattice points
plt.figure(figsize=(6, 6))
plt.scatter(X, Y, color='blue')

# Plot the lattice vectors
plt.quiver(0, 0, a1[0], a1[1], angles='xy', scale_units='xy', scale=1, color='red')
plt.quiver(0, 0, a2[0], a2[1], angles='xy', scale_units='xy', scale=1, color='green')

# Draw the Wigner-Seitz cell
rectangle = Rectangle((-0.5, -0.5), 1, 1, edgecolor='black', facecolor='none')
plt.gca().add_patch(rectangle)

# Set the aspect ratio and limits
plt.gca().set_aspect('equal', adjustable='box')
plt.xlim(-2.5, 2.5)
plt.ylim(-2.5, 2.5)

# Add labels
plt.text(a1[0], a1[1], 'a1', fontsize=12, ha='right')
plt.text(a2[0], a2[1], 'a2', fontsize=12, va='bottom')

plt.show()

import matplotlib.pyplot as plt
import numpy as np
from matplotlib.patches import RegularPolygon

# Define the lattice vectors
a1 = np.array([1, 0])
a2 = np.array([1/2, np.sqrt(3)/2])

# Generate a grid of lattice points
x = np.arange(-2, 3)
y = np.arange(-2, 3)
X, Y = np.meshgrid(x, y)

# Generate the hexagonal lattice points
X_hex = X + Y/2
Y_hex = Y * np.sqrt(3)/2

# Plot the lattice points
plt.figure(figsize=(6, 6))
plt.scatter(X_hex, Y_hex, color='blue')

# Plot the lattice vectors
plt.quiver(0, 0, a1[0], a1[1], angles='xy', scale_units='xy', scale=1, color='red')
plt.quiver(0, 0, a2[0], a2[1], angles='xy', scale_units='xy', scale=1, color='green')

# Draw the Wigner-Seitz cell
polygon = RegularPolygon((0, 0), 6, radius=1/np.sqrt(3), edgecolor='black', facecolor='none')
plt.gca().add_patch(polygon)

# Set the aspect ratio and limits
plt.gca().set_aspect('equal', adjustable='box')
plt.xlim(-2.5, 2.5)
plt.ylim(-2.5, 2.5)

# Add labels
plt.text(a1[0], a1[1], 'a1', fontsize=12, ha='right')
plt.text(a2[0], a2[1], 'a2', fontsize=12, va='bottom')

plt.show()

(b)

3次元六方格子の逆格子点を求めよ。なお、六方格子の基本並進ベクトルは

\[ \begin{aligned} \symbfit{a}_1 &= \frac{\sqrt{3}a}{2} \symbfit{e}_x - \frac{a}{2} \symbfit{e}_y, \\ \symbfit{a}_2 &= \frac{\sqrt{3}a}{2} \symbfit{e}_x + \frac{a}{2} \symbfit{e}_y, \\ \symbfit{a}_3 &= c \symbfit{e}_z \end{aligned} \]

で与えられるとせよ。また、xy面内での格子点と逆格子点の配列をそれぞれ図示せよ。

理論

三次元六方格子の逆格子点の求め方は次のとおり。

\[ \symbfit{b_i} = 2\pi \frac{\symbfit{a_j} \times \symbfit{a_k}}{\symbfit{a_i} \cdot (\symbfit{a_j} \times \symbfit{a_k})} \]

解答

\[ \begin{aligned} \symbfit{b}_1 &= \frac{2\pi}{a} \left( \frac{1}{\sqrt{3}} \symbfit{e}_x - \symbfit{e}_y \right), \\ \symbfit{b}_2 &= \frac{2\pi}{a} \left( \frac{1}{\sqrt{3}} \symbfit{e}_x + \symbfit{e}_y \right), \\ \symbfit{b}_3 &= \frac{2\pi}{c} \symbfit{e}_z \end{aligned} \]

import numpy as np
import matplotlib.pyplot as plt

# Define the lattice vectors
a1 = np.array([np.sqrt(3)/2, -1/2])
a2 = np.array([np.sqrt(3)/2, 1/2])

# Define the reciprocal lattice vectors
b1 = np.array([2 * np.pi / np.sqrt(3), -2 * np.pi])
b2 = np.array([2 * np.pi / np.sqrt(3), 2 * np.pi])

# Generate a grid of lattice points
x = np.arange(-40, 40)
y = np.arange(-40, 40)
X, Y = np.meshgrid(x, y)

# Convert the grid to lattice coordinates
X_lat = X*a1[0] + Y*a2[0]
Y_lat = X*a1[1] + Y*a2[1]

# Convert the grid to reciprocal lattice coordinates
X_rec = X*b1[0] + Y*b2[0]
Y_rec = X*b1[1] + Y*b2[1]

# Plot the lattice points
plt.figure(figsize=(12, 12))
plt.scatter(X_lat, Y_lat, color='blue', label='Lattice points')

# Plot the reciprocal lattice points
plt.scatter(X_rec, Y_rec, color='red', label='Reciprocal lattice points')

# Set the aspect ratio and limits
plt.gca().set_aspect('equal', adjustable='box')
plt.xlim(-10, 10)
plt.ylim(-10, 10)

# Add a legend
plt.legend()

plt.show()

問2

下図に示すような1種類の原子からなる1次元結晶の格子振動を考えよう。

(a)

\(j\) 番目の原子の（古典的）運動方程式を書き下せ。

(b)

\(u_j = A \exp(ikja) \exp(-i\omega t)\) という解を仮定して、上の運動方程式から分散関係を導出せよ。また、その分散関係をブリュアンゾーンの中で図示せよ。

(c)

1次元結晶の単位胞内に異なる2つの原子がある場合の分散関係の概略を図示し、そこに現れるモードについて知るところを述べよ。

理論

一次元のブリルアンゾーンの話だけど、これについては定義 (Section 1.1.4) に立ち戻って、 \(aG_n = 2\pi n\) になるような \(G_n\) の並びを考えれば、ブリルアンゾーンは \([-\pi/a, \pi/a]\) になる。

2種類の原子がある場合はおそらく途中式は必要ないので、ここに少しだけまとめる。2種類の原子の質量をそれぞれ \(M_1, M_2\) とし、バネ定数を \(K\) とすると、運動方程式に次の値を代入する。

\[u_j = U e^{i(kja - \omega t)} \]

\[ v_j = V e^{i(kja + ka/2 - \omega t)} \]

代入して得られた式に \(U,V\) の非自明解条件を求めると、

\[ \begin{aligned} \omega^2(k) &= \frac{K(M_1 + M_2)}{M_1 M_2} \left[ 1 \pm \sqrt{1 - \frac{4 M_1 M_2}{(M_1 + M_2)^2} \sin^2\left( \frac{ka}{2} \right)} \right] \\ &= \frac{K}{\mu} \left[ 1 \pm \sqrt{1-4\frac{\mu}{M}\sin^2\left( \frac{ka}{2} \right)} \right] \end{aligned} \]

解答

普通に運動方程式を立てる。

\[ \begin{aligned} m\ddot{x_j} &= -K(x_j - x_{j-1}) + K(x_{j+1} - x_j) \\ &= - K(2x_j -x_{j+1} - x_{j-1}) \end{aligned} \]

ここで、\(A\) は振幅、\(k\) は波数、\(a\) は格子定数に注意して、

\[ x_j(t) = A e^{i(kja - \omega t)} \]

を代入すると、

\[ m\omega^2 = 2K(1 - \cos(ka)) \]

import numpy as np
import matplotlib.pyplot as plt

# パラメータ設定
m = 1.0  # 質量
K = 1.0  # バネ定数
a = 1.0  # 格子定数

# ブリルアンゾーン内のk
k = np.linspace(-np.pi/a, np.pi/a, 1000)
omega = np.sqrt(2*K/m * (1 - np.cos(k*a)))

# グラフ描画
plt.figure(figsize=(6, 6))
plt.plot(k, omega)

# 軸ラベルにLaTeX表記を使用
plt.xlabel(r"$k$ (wave number)")
plt.ylabel(r"$\omega$ (angular frequency)")
plt.title("Dispersion relation in the first Brillouin zone")

# 軸の目盛りを数式で表す
plt.xticks(
    ticks=[-np.pi/a, -np.pi/(2*a), 0, np.pi/(2*a), np.pi/a],
    labels=[r"$-\frac{\pi}{a}$", r"$-\frac{\pi}{2a}$", r"$0$", r"$\frac{\pi}{2a}$", r"$\frac{\pi}{a}$"]
)
plt.yticks(
    ticks=[0, np.sqrt(4*K/m)],
    labels=[r"$0$", r"$\sqrt{\frac{4K}{M}}$"]
)

plt.grid(True)
plt.tight_layout()
plt.show()

(c)の方については、

\[ \begin{aligned} \omega^2(k) = \frac{K(M_1 + M_2)}{M_1 M_2} \left[ 1 \pm \sqrt{1 - \frac{4 M_1 M_2}{(M_1 + M_2)^2} \sin^2\left( \frac{ka}{2} \right)} \right] \end{aligned} \]

となる。

import numpy as np
import matplotlib.pyplot as plt

# パラメータ設定
M1 = 1.0
M2 = 2.0
K = 1.0
a = 1.0

# 波数ベクトル（ブリルアンゾーン内）
k = np.linspace(-np.pi/a, np.pi/a, 1000)

# 定数計算
A = K * (M1 + M2) / (M1 * M2)
B = 4 * M1 * M2 / (M1 + M2)**2
sin_term = np.sin(k * a / 2)**2

# 分散関係（アコースティック・オプティカルモード）
omega_sq_plus = A * (1 + np.sqrt(1 - B * sin_term))
omega_sq_minus = A * (1 - np.sqrt(1 - B * sin_term))

omega_plus = np.sqrt(np.real(omega_sq_plus))
omega_minus = np.sqrt(np.real(omega_sq_minus))

# グラフ描画
plt.figure(figsize=(6, 6))
plt.plot(k, omega_plus, label="Optical mode", linewidth=2)
plt.plot(k, omega_minus, label="Acoustic mode", linewidth=2)

# 軸ラベルにLaTeX表記を使用
plt.xlabel(r"$k$ (wave number)")
plt.ylabel(r"$\omega$ (angular frequency)")
plt.title("Dispersion relation (diatomic 1D lattice)")

# 軸の目盛り（対称に数式で）
plt.xticks(
    ticks=[-np.pi/a, -np.pi/(2*a), 0, np.pi/(2*a), np.pi/a],
    labels=[r"$-\frac{\pi}{a}$", r"$-\frac{\pi}{2a}$", r"$0$", r"$\frac{\pi}{2a}$", r"$\frac{\pi}{a}$"]
)

# 最大振動数の目安
omega_max = np.max(omega_plus)
plt.yticks(
    ticks=[0, omega_max],
    labels=[r"$0$", r"$\omega_{\mathrm{max}}$"]
)

plt.legend()
plt.grid(True)
plt.tight_layout()
plt.show()

問3

固体中の電子に関して以下の問いに答えよ。

(a)

1辺の長さ \(L\) の立方体中の \(N\) 個の自由電子を考えよう。

i.

自由電子モデルでは、エネルギー \(E\) と波数 \(k\) の関係により状態密度が

\[ D(E) = \frac{L^3}{2\pi^2} \left( \frac{2m_e}{\hbar^2} \right)^{3/2} \sqrt{E} \]

で与えられることを示せ。

ii.

フェルミエネルギー \(E_F\) を電子数 \(N\) の関数として与えよ。状態密度を使って計算すること。

---

(b)

格子定数 \(a\) で（1種類の原子）からなる1次元結晶を考える。2つの原子軌道（1s, 2s）のみを考慮すると、強結合近似では

\[ \sum_n \sum_{\mu = 1s, 2s} c_{\mu} e^{ika(n - n')} \left( \langle n'\mu' | \hat{H} | n\mu \rangle - E \langle n'\mu' | n\mu \rangle \right) = 0 \]

が成り立つ（ここで \(n\) は単位胞の番号である）。最近接原子の同種原子軌道間の相互作用以外を無視でき、

\[ \langle n'\mu' | \hat{H} | n\mu \rangle = \begin{cases} E_{1s} & (n = n',\ \mu = \mu' = 1s) \\ E_{2s} & (n = n',\ \mu = \mu' = 2s) \\ t_{1s} & (n = n' \pm 1,\ \mu = \mu' = 1s) \\ t_{2s} & (n = n' \pm 1,\ \mu = \mu' = 2s) \\ 0 & \text{(それ以外)} \end{cases} \]

\[ \langle n'\mu' | n\mu \rangle = \begin{cases} 1 & (n = n',\ \mu = \mu') \\ 0 & \text{(それ以外)} \end{cases} \]

であるとしてバンド分散を求めよ。さらに、このバンド分散の概形を、\(t_{1s} > 0,\ t_{2s} < 0\) としてブリュアンゾーン内で描け。

理論

(a)は Section 1.2.2 ここら辺を読めばいい。一応軽くまとめる。

波数空間で、 \((2\pi/L)^3\) ごとに一個の状態があるから、体積あたりの状態数は \(1/(2\pi/L)^3\) になる。

次に波数空間の球体を考えて

\[ \frac{4\pi}{3} k^3 = \frac{4\pi}{3} \left( \frac{2m_e}{\hbar^2} E \right)^{3/2} \]

これに密度と、電子スピンの自由度2をかけてやって

\[ N(E) = \frac{L^3}{3\pi^2} \left( \frac{2m_e E}{\hbar^2} \right)^{3/2} \]

これを微分してやると、状態密度が出てくる。この密度をフェルミエネルギーまで積分したら状態数 \(N\) になるのは定義。

2. については、Section 1.3 で軽くまとめた。実際に問題を解く際に気をつけるべきは、\(\sum\) しているのは、 \(n,\ \mu\) だけであって、 \(n',\ \mu'\) はその都度代入して考えているところ。実際に手を動かせばわかるはず。

解答

\[ \begin{aligned} D(E)\dd E &= 2 \times 4\pi k^2 \dd k \times \frac{1}{(2\pi/L)^3} \\ &= \frac{L^3}{2\pi^2} \left( \frac{2m_e}{\hbar^2} \right)^{3/2} \sqrt{E} \dd E \end{aligned} \]

\[ \begin{aligned} \int _0^{E_F} D(E) \dd E &\triangleq N \\ E_F &= \frac{\hbar^2}{2m_e} \left( \frac{3\pi^2 N}{L^3} \right)^{2/3} \\ \end{aligned} \]

\(\mu = \mathrm{1s}\) の場合、

\[ \begin{aligned} \mathcal{E}_{\mathrm{1s}} &= E_{\mathrm{1s}} + 2t_{\mathrm{1s}} \cos(ka) \\ \mathcal{E}_{\mathrm{2s}} &= E_{\mathrm{2s}} + 2t_{\mathrm{2s}} \cos(ka) \\ \end{aligned} \]

ここで、 \(n'\) は最近接原子の単位胞の番号。

import numpy as np
import matplotlib.pyplot as plt

# パラメータの設定（必要に応じて変更してください）
a = 1.0       # 格子定数
E1s = 0.0     # 1s 軌道のオンサイトエネルギー
t1s = 1.0     # 1s 軌道のホッピング積分 (t1s > 0)
E2s = 1.0     # 2s 軌道のオンサイトエネルギー
t2s = -0.5    # 2s 軌道のホッピング積分 (t2s < 0)

# k の範囲を第一ブリュアンゾーン内で設定
k = np.linspace(-np.pi/a, np.pi/a, 400)

# バンド分散を計算
E_1s = E1s + 2 * t1s * np.cos(k * a)
E_2s = E2s + 2 * t2s * np.cos(k * a)

# プロット
plt.figure()
plt.plot(k * a, E_1s, label='1s')
plt.plot(k * a, E_2s, label='2s')
plt.xlabel('ka')
plt.ylabel('E')
plt.title('Band dispersion of 1D crystal')
plt.legend()
plt.grid(True)
plt.show()

2019年度

問3(b)

周期ポテンシャル

\[ V(x) = V_1 \cos\!\Bigl(\frac{2\pi}{a}x\Bigr) \]

で電子の振る舞いを考える。ブリュアンゾーン端 (\(k = \pi/a\)) で電子波 \(\exp(ikx)\) はブラッグ反射され、その結果 \(\exp(i k x)\) と \(\exp(-i k x)\) が重畳した 2 種類の定在波が形成される。

波動関数：

\[ \phi_+(x) = \frac{1}{\sqrt{2a}}\Bigl\{e^{i\frac{\pi}{a}x}+e^{-i\frac{\pi}{a}x}\Bigr\} = \sqrt{\frac{2}{a}}\cos\!\Bigl(\frac{\pi}{a}x\Bigr) \]

\[ \phi_-(x) = \frac{1}{\sqrt{2a}}\Bigl\{e^{i\frac{\pi}{a}x}-e^{-i\frac{\pi}{a}x}\Bigr\} = i\,\sqrt{\frac{2}{a}}\sin\!\Bigl(\frac{\pi}{a}x\Bigr) \]

（これらの波動関数は単位胞 \(0 \le x \le a\) の範囲で規格化されている。）

i.

\(|\phi_+(x)|^2\) と \(|\phi_-(x)|^2\) を求め、\(V(x)\) とともに図示せよ。

ii.

2つの状態 \(\phi_+(x)\) と \(\phi_-(x)\) のエネルギー期待値の差を計算せよ。
> ※ これらは固有関数ではないので固有エネルギーを求めようとしてはいけない。
> また、個々の状態の期待値を計算するより、期待値の差を直接計算する方がやさしい。

iii.

以上の結果に基づき、結晶のエネルギーバンド構造形成のメカニズムを論ぜよ。

理論

やることは基本的な波動関数の操作。ただ、固有関数、固有エネルギーじゃないのに、色々と議論を進めるせいで混乱する可能性がある。これは詳しくは書かないが、近侍として扱っていると思っておけば良さそうだ。

解答

1. 単純計算すれば、 \[ \begin{aligned} |\phi_+(x)|^2 &= \frac{2}{a} \cos^2\!\Bigl(\frac{\pi}{a}x\Bigr) \\ |\phi_-(x)|^2 &= \frac{2}{a} \sin^2\!\Bigl(\frac{\pi}{a}x\Bigr) \\ \end{aligned} \]

import numpy as np
import matplotlib.pyplot as plt

# パラメータ設定
a = 1.0
V1 = 1.0

# x座標
x = np.linspace(0, a, 500)

# 確率密度とポテンシャル
phi_plus_sq = (1/a)*(1 + np.cos(2*np.pi*x/a))
phi_minus_sq = (1/a)*(1 - np.cos(2*np.pi*x/a))
V = V1 * np.cos(2*np.pi*x/a)

# プロット
plt.figure()
plt.plot(x, phi_plus_sq, label=r'$|\phi_+(x)|^2$')
plt.plot(x, phi_minus_sq, label=r'$|\phi_-(x)|^2$')
plt.plot(x, V, label=r'$V(x)$')
plt.xlabel('x')
plt.ylabel('Probability density / Potential')
plt.title('|\u03C6_+|^2, |\u03C6_-|^2 and V(x)')
plt.legend()
plt.tight_layout()
plt.show()

2. \[ \hat{H}\phi_{\pm}(x) = E_0 \phi_{\pm}(x) \] を満たすことから、次のような計算が可能である。 \[ \begin{aligned} \Delta E &= \bra{\phi_+(x)} \hat{H} \ket{\phi_+(x)} - \bra{\phi_-(x)} \hat{H} \ket{\phi_-(x)} \\ &= V(x)\qty{\bra{\phi_+^{\ast}(x)}\ket{\phi_+(x)} - \bra{\phi_-^{\ast}(x)}\ket{\phi_-(x)}} \\ &= \int_0^a V(x) \qty{\frac{2}{a}\cos^2 \frac{\pi}{a}x - \frac{2}{a}\sin^2 \frac{\pi}{a}x} \dd x \\ &= \frac{2V_1}{a} \int_0^a \cos^2 \frac{2\pi}{a}x \dd x \\ &= V_1 \end{aligned} \]
3. \(\phi_+\) ではポテンシャルが高い場所での電子存在確率が高くなり、電子エネルギーが高く、 \(\phi_-\) ではポテンシャルが低い場所での電子存在確率が高くなり、電子エネルギーが低くなる。このようにポテンシャルの周期性がバンドギャップの原因となる。

2021年度

問3(b)

下に示した右図は GaAs（閃亜鉛鉱構造、ブラベ格子は面心立方格子、慣用単位胞の格子定数 \(a = 0.57\,\mathrm{nm}\)）の価電子帯と伝導帯近傍のバンド構造である。
赤色の一点鎖線は、下から4番目のバンドの \(k=0\) 付近での二次関数フィッティングである。

i. 逆格子点の導出

一辺の長さ \(a\) の立方体を慣用単位胞とする面心立方格子の基本並進ベクトルは次の通りとする。

\[ \mathbf{a}_1 = \frac{a}{2}\,\mathbf{e}_y + \frac{a}{2}\,\mathbf{e}_z,\quad \mathbf{a}_2 = \frac{a}{2}\,\mathbf{e}_x + \frac{a}{2}\,\mathbf{e}_z,\quad \mathbf{a}_3 = \frac{a}{2}\,\mathbf{e}_x + \frac{a}{2}\,\mathbf{e}_y. \]

• これらから逆格子ベクトル \(\mathbf{b}_i\) を求めよ。
  
• 得られた逆格子点の配列のブラベ格子の名称と、その慣用単位胞の一辺の長さを答えよ。

ii. 電子の有効質量

GaAs の電子の有効質量を計算し，電子の静止質量と比較せよ。
計算の過程も明示すること。

iii. 有効質量と電気伝導度の比較

以下の語句を必ず用いて説明せよ：
- 自由電子
- 状態密度
- フェルミ準位
- 移動度

1. なぜ多くの半導体の電子有効質量が金属に比べて小さくなるのか
   
2. なぜ金属に比べて半導体の電気伝導度が著しく小さいのか

理論

2. この式を使えばいい。 \[ \begin{aligned} E(k) &= \frac{\hbar^2}{2m} k^2 \\ \frac{1}{m^*} &= \frac{1}{\hbar^2}\frac{d^2E(k)}{dk^2} \end{aligned} \]

解答

1. \[ \begin{aligned} \symbfit{b}_1 &= \frac{2\pi}{a}\bigl(-\symbfit{e}_x + \symbfit{e}_y + \symbfit{e}_z\bigr),\\ \symbfit{b}_2 &= \frac{2\pi}{a}\bigl(\symbfit{e}_x - \symbfit{e}_y + \symbfit{e}_z\bigr),\\ \symbfit{b}_3 &= \frac{2\pi}{a}\bigl(\symbfit{e}_x + \symbfit{e}_y - \symbfit{e}_z\bigr). \end{aligned} \] これは一辺 \(4\pi/a\) のBCCである。

2. \[ E = \alpha k^2 \] とすると、 \[ m = \frac{\hbar^2}{2\alpha} \] となる。グラフの形状が読み取りづらいので、続きは各自で解かれたし。

1. 半導体の伝導帯では，原子間の反強結合性軌道からなるバンドのバンド曲率が大きくなるため。

2. 半導体ではフェルミ準位がバンドギャップ内に位置し、伝導帯中の電子濃度が小さいため、電気伝導度が小さい。

References

矢口裕之. 2017. “初歩から学ぶ固体物理学.”