1
| 難易度 | 所要時間 |
|---|---|
| C | 20分 |
問題
次の値の1の桁の数を求めよ。
\[ \left\lfloor \frac{10^{20000}}{10^{100}+3} \right\rfloor \]
解答
\(N\) を次のように定義する
\[ N=\frac{10^{20000}-(-3)^{200} }{100^{100} - (-3)} = (100^{100})^{199} - 3 \times (100^{100})^{198} + ... - 3^{199} \]
となるので、
\[ \frac{10^{20000}}{10^{100}+3} = N + \frac{3^{200} }{10^{100} + 3} \]
ここで、
\[ \frac{3^{200} }{10^{100} + 3} < 1 \]
なので、
\[ \left\lfloor \frac{10^{20000}}{10^{100}+3} \right\rfloor = N \]
とわかる。ここで、\(N\) を \(10\) を法にして考えれば、
\[ N \equiv -3^{199} \equiv -27 \times 81 ^{49} \equiv 3 \]
となり、答えは \(3\) となる。
2
| 難易度 | 所要時間 |
|---|---|
| C | 20分 |
問題
1
次の連立方程式の解を \((x,y)\) として、 \(z=x+yi\) とおく。
\[\begin{eqnarray} \left\{ \begin{array}{l} \dfrac{x}{x^2+y^2}=1 \\ -\dfrac{y}{x^2+y^2}=1 \end{array} \right. \end{eqnarray}\]
次の等式を示せ。
\[ z^{-1} = 1 + i \]
2
次の4つの集合を考える。
\[\begin{align*} A &= \left\{ (x,y): x^2 - y^2 = \frac{x}{x^2+y^2} +1 \right\} \\ B &= \left\{ (x,y): 2xy = -\frac{y}{x^2+y^2} \right\} \\ C &= \left\{ (x,y): x^3-3xy^2 = 1+x \right\} \\ D &= \left\{ (x,y): 3x^2y-y^3 = y \right\} \end{align*}\]
この時、 \(A \cap B = C \cap D\) であることを示せ。
解答
1
\(z=x+yi\) として、 \(z^{-1} = 1 + i\) を計算すると、実部と虚部がそれぞれ与えられた式になることがわかる。
2
\(z = x + yi\) としたとき、\(A \cap B\) は \(z^2 = z^{-1} + 1\) の実部と虚部を表しており、 \(C \cap D\) は \(z^3 = 1 + z\) の実部と虚部を表している。
3
| 難易度 | 所要時間 |
|---|---|
| B | 20分 |
問題
\(A,B,C\) を \(xy\) 平面上の点として、それぞれの座標は整数値であるとする。この時、次の不等式が成り立つのは、3点が正方形の頂点であるとき、その時に限ることを示せ。
\[ (|AB|+|BC|) ^2 < 8 \cdot [ABC] + 1 \]
ただし、 \(|AB|\) は \(A,B\) の距離、 \([ABC]\) は \(A,B,C\) で張られる三角形の面積を表す。
解答
2
| 難易度 | 所要時間 |
|---|---|
| B | 20分 |
問題
下図のように、お互いの中心が \(r\) だけ離れた、半径 \(r\) の2つの円がある。
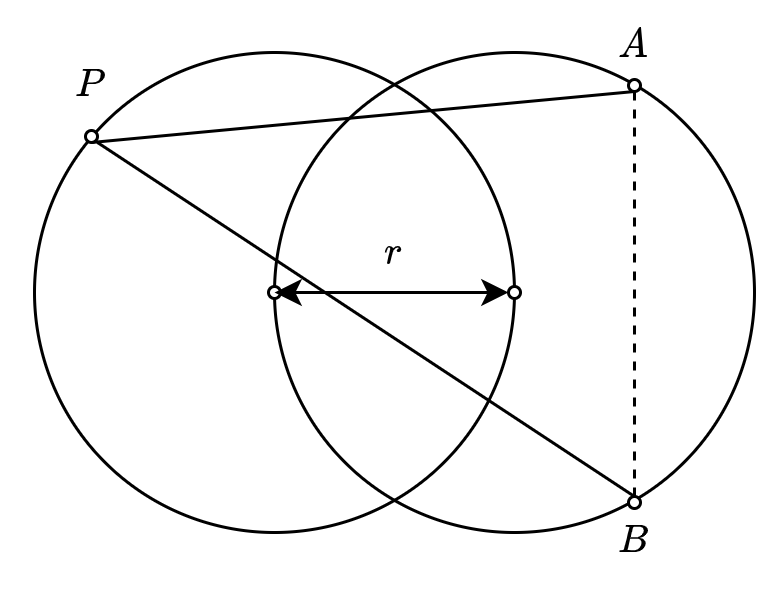
この時、片方の円に、円の中心同士の結ぶ線に対して対称的な位置にある点を \(A,B\) とする。また、 \(P\) はもう片方の円の周上にあるとするとき、次の不等式を示せ。
\[ PA^2 + PB^2 \geq 2r^2 \]
解答
右の円の中心を \(O\) として、 \(AB\) の中点を \(C\) とすると、
\[ PA^2 + PB^2 = 2PC^2 + 2AC^2 \geq 2OC^2 + 2AC^2 = 2OA^2 = 2r^2 \]
となる。等号成立条件は \(P\) が \(O\) である時である。